Bubblesort ist ein einfacher Sortieralgorithmus zum Sortieren von Listen und Arrays. Bubbble Sort hat eine quadratische Laufzeitkomplexität. Der Algorithmus wurde Bubble Sort genannt, weil das Verschieben der größten Elemente bis zum Ende des unsortierten Teils des Arrays an an die Obefläche aufsteigende Luftblasen erinnert.
Funktionsweise
Grundidee:
Das Array besteht aus einem unsortierten Teil gefolgt von einem sortierten Teil. Zu Beginn befinden sich noch alle Elemente im unsortierten Teil. In jeder Iteration werden alle Elemente des unsortierten Teilarrays durchgegangen und das bisher in der Iteration größte gefundene Element wird weitergereicht, bis am Ende der Iteration das letzte Element des unsortierten Teilarrays das größte Element aus diesem unsortierten Bereich enthält.
Pseudocode:
Vorgehen:
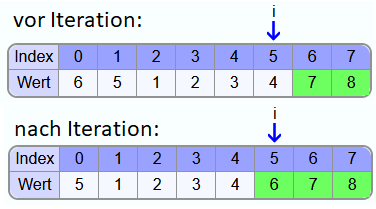
Am Anfang ist i der Index vom letzten Element im Array. Vor jeder Iteration der äußeren Schleife ist das Teilarray, welches von Index 0 bis Index i verläuft, unsortiert, das Teilarray ab Index i+1 bis zum Ende ist sortiert und alle Elemente im sortierten Teil sind an ihrer finalen Position. Nach jeder Iteration soll das größte Element aus dem unsortierten Teil in das Feld mit dem Index i verschoben worden sein. Da die Elemente hinter dem Element mit dem Index i nicht verändert werden und das Element an der Stelle i größer oder gleich von jedem Element mit kleinerem Index ist, sind somit am Ende der Iteration alle Elemente ab Index i an ihrer finalen Position.
Die innere Schleife beginnt mit dem ersten Element des Arrays und läuft bis zum Element vor dem Element mit dem Index i. Vor jeder Iteration der inneren Schleife enthält das Feld mit dem Index j das größte Element aus dem Teilarray von 0 bis j. Wenn das Element an der Stelle j größer ist als das Element an der Stelle j+1, werden die beiden Elemente vertauscht. Somit enthält am Ende der Iteration das Element mit dem Index j+1 das größte Element im Bereich von 0 bis j+1. Insbesondere enthält am Ende der Iteration mit j = i-1 das Feld mit dem Index i den größten Wert aus dem Bereich Index 0 bis i.
Beispiel:
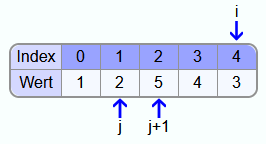
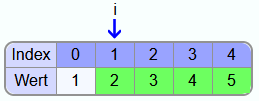
Iteration 1:
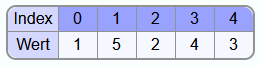
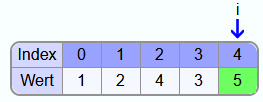
Als Beispiel soll das folgende Array sortiert werden:
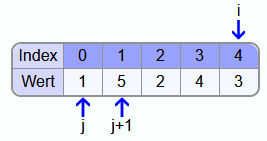
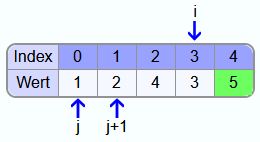
Als erstes wird i auf den Index vom letzten Element gesetzt und j beginnt mit dem ersten Element vom Array. Da die 1 nicht größer ist als die 5 werden die beiden Zahlen nicht vertauscht.
Danach wird j eins weiter nach rechts gesetzt und es werden die 5 und die 2 verglichen. Da 5 größer ist, müssen die beiden Zahlen vertauscht werden.
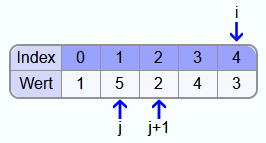
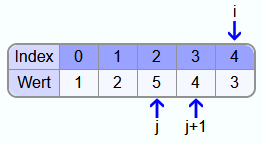
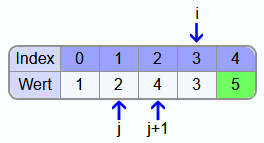
5 ist auch größer als 4. Somit müssen auch diese beiden Zahlen vertauscht werden.
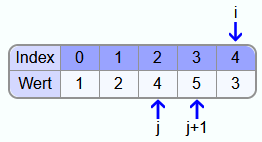
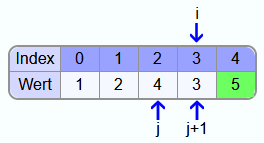
Danach müssen noch die 5 und die 3 vertauscht werden.
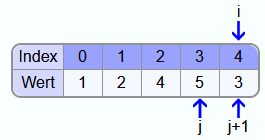
Am Ende der ersten Iteration ist das letzte Element, also die 5, an der finalen Position.
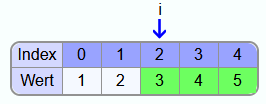
Iteration 2:
i wird 1 Feld weiter nach links gesetzt und j beginnt wieder bei 0.
Da 1 nicht größer ist als 2 müssen die beiden Elemente nicht vertauscht werden.
Ebenso im darauf folgenden Iterationsschritt:
Die 4 und die 3 müssen vertauscht werden.
Am Ende der zweiten Iteration sind die letzten beiden Elemente an ihrer finalen Position.
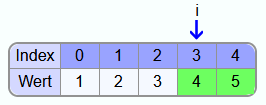
Iteration 3:
1 ist nicht größer als 2 und 2 ist nicht größer als 3. Somit muss in Iteration 3 nichts vertauscht werden und die 3 ist an der finalen Position.
Iteration 4:
1 ist nicht größer als 2 und somit ist die 2 schon auf der richtigen Position.
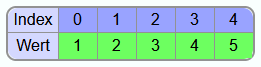
Ergebnis:
Es ist nur noch 1 Element übrig, welches sortiert werden muss. Da ein Teilarray mit nur einem Element automatisch sortiert ist, ist auch das erste Element an der richtigen Position und das gesamte Array ist sortiert.
umgekehrte Sortierreihenfolge
Der Bubblesort Algorithmus lässt sich sehr einfach so anpassen, dass die Elemente in absteigender Reihenfolge sortiert werden. Um dies zu erreichen, müssen die Elemente vertauscht werden, wenn A[j+1] größer als A[j] ist.