Mit Dijkstras Algorithmus lassen sich die kürzesten Wege von einem Startknoten zu jedem Knoten des Graphen berechnen. Der Algorithmus lässt sich sowohl auf gerichtete als auch auf ungerichtete Graphen anwenden. Wichtig ist aber, dass die Kantengewichte nicht negativ sein dürfen.
Anwendung
Ein klassisches Anwendungsgebiet für den Dijkstra-Algorithmus ist die Routenplanung. Dabei modellieren Knoten Kreuzungen. Also Stellen, an denen man sich für eine Richtung entscheiden kann. Kanten modellieren die Straßen zwischen den Kreuzungen. Die Kantengewichte können die Dauer sein, die man zum Zurücklegen der Strecke zwischen 2 Kreuzungen benötigt. Je nach Anwendungsgebiet kann es aber auch sinnvoll sein zum Beispiel die zurückgelegte Strecke oder den Spritverbrauch mit einzuberechnen.
Funktionsweise
Pseudocode:
Eingabe:
Der Dijkstra-Algorithmus erhält eine Menge von Knoten V, eine Menge von Kanten E und einen Startknoten start∈V.
Wichtige Werte und Mengen:
Es wird eine Menge von Knoten Q⊆V benötigt, welche alle Knoten enthält, zu denen potentiell noch kein kürzester Pfad gefunden wurde.
Jeder Knoten v∈V bekommt einen Distanzwert distanz[v] zugewiesen. Dieser ist die Länge des kürzesten Pfades vom Startknoten start zum Knoten v, auf dem höchstens v noch in Q enthalten sein darf. Wenn ein solcher Pfad nicht existiert, ist distanz[v]=∞.
Außerdem gibt es für jeden Knoten v∈V einen Vorgänger vorgänger[v]. Wenn ein Pfad gefunden wurde, welcher, abgesehen eventuell von v selber, nur Knoten enthält, die schon aus Q entfernt wurden, dann ist vorgänger[v] der direkte Vorgänger von v auf diesem Pfad. Ansonsten ist vorgänger[v]=null. Mit der Hilfe dieser Vorgängerwerte lässt sich der Pfad von v nach start zurückverfolgen.
Ziel:
Nach der Ausführung des Algorithmus enthält für jedes v∈V, wenn es einen Pfad von start nach v gibt, distanz[v] die Länge des kürzesten Pfades von start nach v und vorgänger[v] ist der direkte Vorgängerknoten auf dem Pfad. Wenn es einen solchen Pfad nicht gibt, bleiben distanz[v]=∞ und vorgänger[v]=null.
Initialisierungsphase:
Dem Startknoten wird der Distanzwert 0 zugewiesen, alle anderen bekommen als Distanzwert ∞.
Alle Knoten erhalten als Vorgängerknoten null zugewiesen.
Alle Knoten werden in Q eingefügt.
Schleife:
In jedem Schleifendurchlauf wird zuerst das Element u∈Q mit dem niedrigsten Distanzwert distanz[u] aus Q extrahiert. Danach wird für jeden direkten Nachfolgerknoten v∈Q von u untersucht, ob der Pfad von start nach v über u kürzer ist, als der bislang gefundene kürzeste Pfad. Wenn dies der Fall ist, wird der Distanzwert von v auf die Länge des Pfades von start nach v über u gesetzt (distanz[v] := distanz[u] + gewicht(u, v)) und u wird der neue Vorgängerknoten von v. Der neue bisher gefundene kürzeste Pfad von start nach v verläuft somit über u mit u als direkten Vorgänger von v.
Dies wird so lange durchgeführt, bis Q leer ist.
kleines Beispiel:
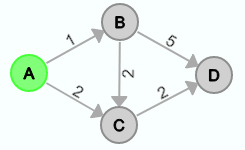
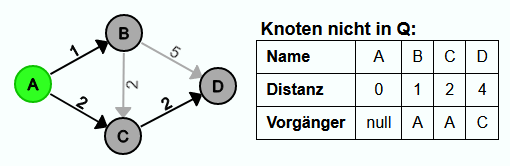
Gegeben sei der folgende kleine Beispielgraph mit A als Startknoten.
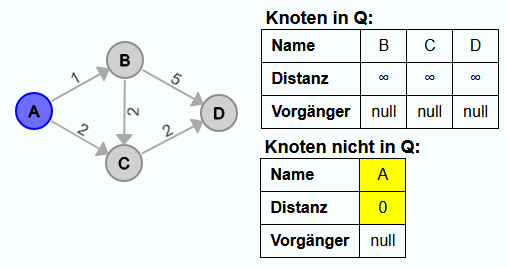
Initialisierung:
Als erstes werden alle Knoten so wie oben beschrieben initialisiert und in Q eingefügt.
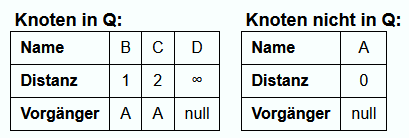
Iteration 1:
In der ersten Iteration ist der Startknoten A der Knoten mit dem kleinsten Distanzwert. Er ist der einzige Knoten, dessen Distanzwert nicht ∞ ist.
Da für B und C noch kein Pfad gefunden wurde und der Distanzwert somit ∞ ist, wird A der neue Vorgängerknoten von B und C und die Distanzwerte werden angepasst.
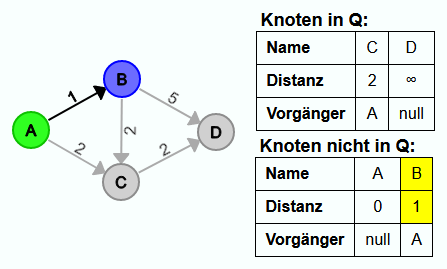
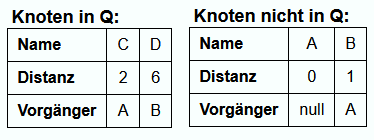
Iteration 2:
Jetzt ist B der Knoten mit dem kleinsten Distanzwert in Q. Also wird er aus Q gelöscht.
Zu D wurde vorher noch kein Pfad gefunden. Also wird B zum neuen Vorgängerknoten von D und der Distanzwert von D wird angepasst.
Der Pfad von A nach C über B ist länger, als der bisher kürzeste Pfad. Also bleibt A der Vorgänger von C.
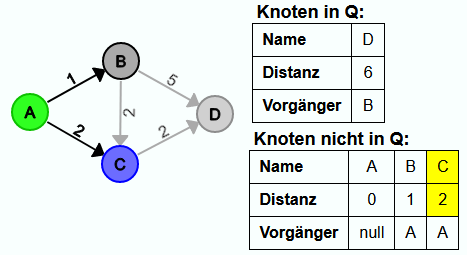
Iteration 3:
Der Distanzwert von C ist kleiner als der von D. Also wird diesmal C aus Q entfernt.
Der Pfad von A nach D über C hat eine Länge von 4 und das ist kürzer als der bisher gefundene kürzeste Pfad mit einer Länge von 6. Somit wird der Pfad über C zum neuen kürzesten Pfad. Also wird der Distanzwert von D auf die Länge des Pfades von A nach C + dem Kantengewicht von C nach D gesetzt und C wird der neue Vorgänger.
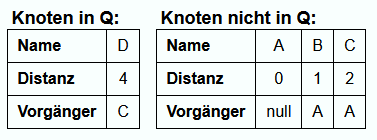
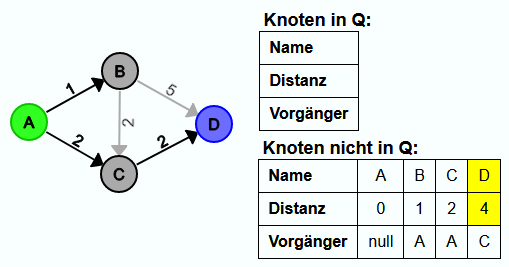
Iteration 4:
D ist das einzige Element in Q und somit auch das mit dem kürzesten Distanzwert. Deshalb wird jetzt D aus Q entfernt.
Q ist nun leer. Jedem Knoten ist jetzt die Länge des kürzesten Pfades von A zum Knoten zugewiesen und über die Vorgänger lassen sich die Pfade rekonstruieren.
Implementationshinweise
Prioritätswarteschlange:
Aus Gründen der Effizenz wird für Q häufig eine sogenannte Prioritätswarteschlange verwendet.
Adjazenzliste:
Häufig werden Graphen als Adjazenzlisten gespeichert. Dafür wird für jeden Knoten eine Liste von Nachfolgerknoten (bzw. im Fall von ungerichteten Graphen Nachbarknoten) und den Kantengewichten abgespeichert. Der Dijkstra-Algorithmus lässt sich gut auf Adjazenzlisten anwenden.
Modifikationen
festes Ziel:
In der Praxis möchte man häufig nicht die kürzesten Wege zu allen Knoten bestimmen, sondern nur zu einem ganz bestimmten. Wenn dieser erreicht ist, kann der Algorithmus abgebrochen werden.
mehrere Startknoten:
Es gibt Anwendungsfälle, bei denen mehr als ein Startknoten sinnvoll ist. Zum Beispiel könnte ein Unternehmen ein Produkt, welches an mehreren Standorten des Unternehmens vorrätig ist, an einen Kunden liefern wollen. Alle diese Standorte könnten mögliche Startknoten sein. In diesem Fall kann man den Dijkstra-Algorithmus so abändern, dass man ihm eine Menge von Startknoten übergibt. In der Initialisierungsphase muss dann jedem der Knoten in der Startknotenmenge der Distanzwert 0 zugewiesen werden.
Abbruch, wenn nur noch unerreichbare Knoten in Q:
Wenn der Knoten in Q mit dem kleinsten Distanzwert den Distanzwert ∞ hat heißt das, dass der Knoten nicht vom Startknoten aus erreicht werden kann. Da es in Q keinen Knoten mit einem geringeren Distanzwert mehr geben kann, sind auch alle anderen Knoten in Q nicht mehr vom Startknoten aus erreichbar. Somit kann der Dijkstra-Algorithmus abgebrochen werden.
nicht alle Knoten in Q
Man muss nicht alle Knoten von Anfang an in Q einfügen. Man kann auch nur den Startknoten einfügen und wenn von dem gerade betrachteten kleinsten Element eine Kante zu einem Knoten führt, der weder in Q ist noch schonmal darin war, wird dieser in Q eingefügt. Dadurch befinden sich in der Praxis häufig weniger Knoten gleichzeitig in Q wodurch sich die verwendete Datenstruktur häufig effizienter verwalten lässt.