Das Sieb des Eratosthenes ist ein Algorithmus, mit dem sich alle Primzahlen bis zu einer vorgegebenen Zahl bestimmen lassen. Diese Zahl wird im Folgenden N genannt.
Auf dieser Seite lässt sich das Sieb des Eratosthenes für Zahlen bis 1000 visualisieren.
Funktionsweise
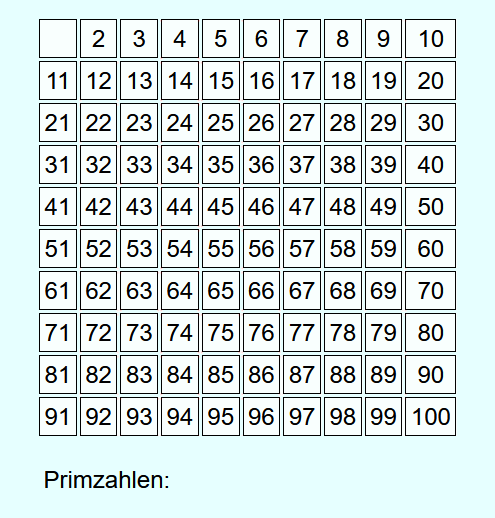
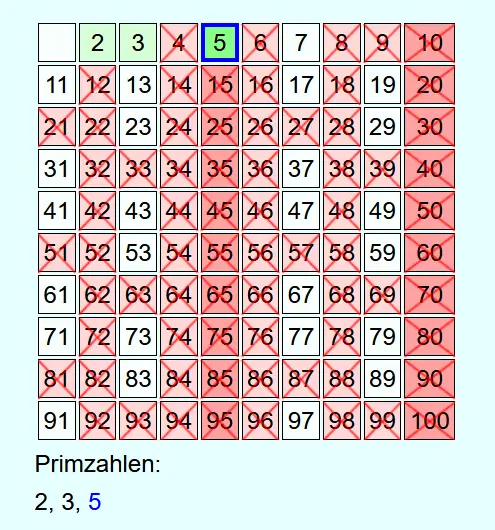
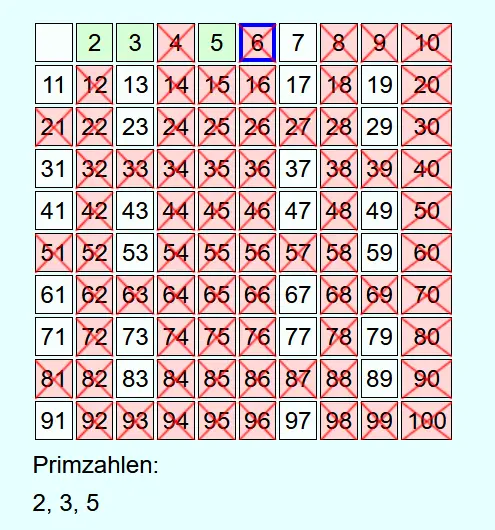
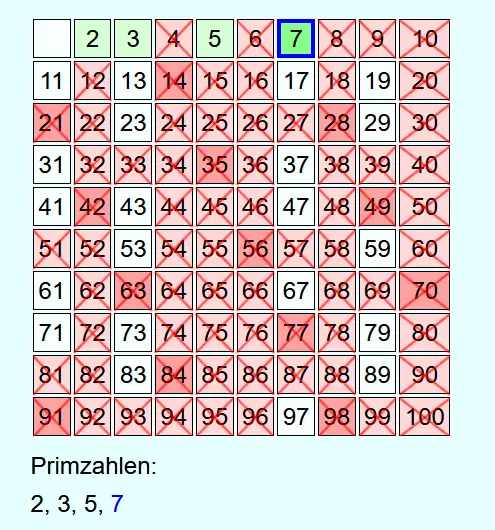
Als Erstes werden alle Zahlen von 2 bis zur vorgegebenen Zahl N aufgeschrieben. Danach werden von 2 beginnend die Zahlen aufsteigend durchgegangen.
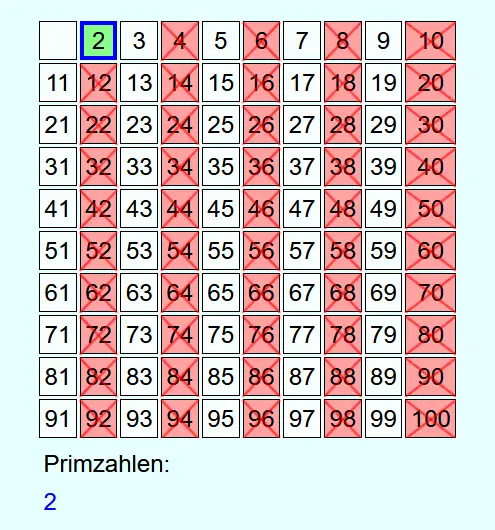
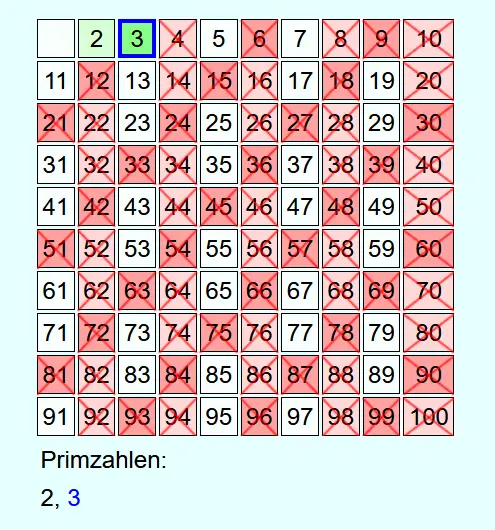
Immer, wenn eine Zahl nicht durchgestrichen ist, dann handelt es sich um eine Primzahl. Diese wird in die Liste der gefundenen Primzahlen aufgenommen und alle Vielfachen dieser Primzahl bis N werden durchgestrichen.
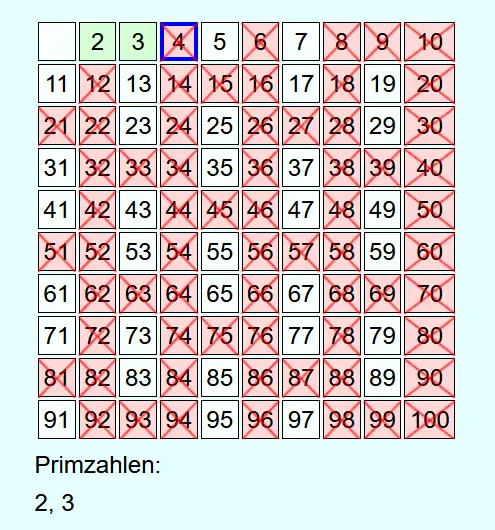
Wenn die aktuelle Zahl durchgestrichen ist, dann handelt es sich um keine Primzahl und es wird nichts weiter damit gemacht.
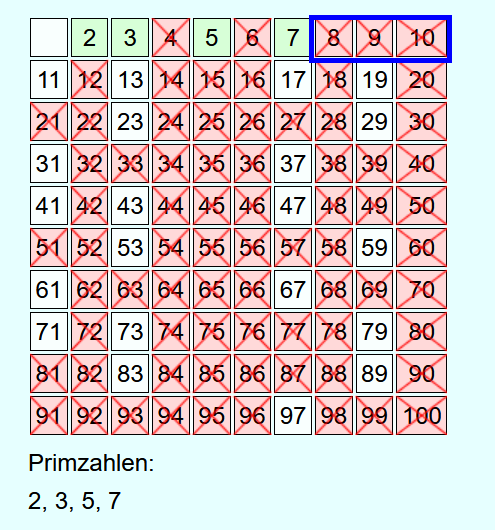
Wenn die aktuelle Zahl größer als N ist, dann wurden schon alle Zahlen bis N, die keine Primzahlen sind, durchgestrichen. Deshalb können die restlichen nicht durchgestrichenen Zahlen in die Liste der gefundenen Primzahlen aufgenommen werden, ohne dass ihre Vielfachen durchgestrichen werden müssen.
Beispiel
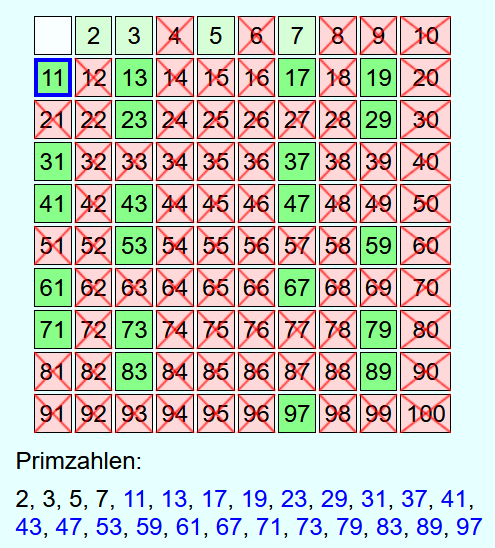
Als Beispiel sollen alle Primzahlen bis 100 ermittelt werden.
Begründungen
Warum handelt es sich um keine Primzahl, wenn die gerade betrachtete Zahl durchgestrichen ist?
Wenn die gerade betrachtete Zahl durchgestrichen ist, dann gab es in einem der vorherigen Schritte eine Zahl, die größer als 1 und kleiner als die gerade betrachtete Zahl ist und die Teiler von der gerade betrachteten Zahl ist. Somit ist die gerade betrachtete Zahl keine Primzahl.
Warum müssen die Vielfachen von Zahlen, die durchgestrichen sind, nicht durchgestrichen werden?
Wenn die gerade betrachtete Zahl durchgestrichen ist, dann existiert mindestens eine kleinere Zahl, die größer als 1 ist und die Teiler von der gerade betrachteten Zahl ist. Da jedes Vielfache einer Zahl auch Vielfaches der Teiler dieser Zahl ist, sind die Vielfachen von der durchgestrichenen gerade betrachteten Zahl bereits durchgestrichen.
Warum handelt es sich um eine Primzahl, wenn die gerade betrachtete Zahl nicht durchgestrichen ist?
Wenn die gerade betrachtete Zahl nicht durchgestrichen ist, dann gibt es keine Zahl, die größer als 1 und kleiner als die gerade betrachtete Zahl ist und die Teiler von der gerade betrachteten Zahl ist. Ansonsten wäre die gerade betrachtete Zahl schon in einem der vorherigen Schritte durchgestrichen worden. Somit handelt es sich bei der gerade betrachteten Zahl um eine Primzahl.
Warum wurden schon alle Zahlen, die keine Primzahlen sind, durchgestrichen, wenn die aktuelle Zahl größer als N ist?
Wenn man 2 oder mehr Zahlen multipliziert, die alle größer als N sind, dann erhält man eine Zahl, die größer als N ist. Deshalb enthält die Primfaktorzerlegung jeder Zahl, die kleiner oder gleich N ist, mindestens einen Primfaktor, der kleiner oder gleich N ist. Wenn die aktuelle Zahl größer als N ist, dann wurden schon alle Vielfachen von Zahlen, die kleiner oder gleich N sind, durchgestrichen. Somit kann es keine Zahlen, die kleiner oder gleich N sind, geben, die keine Primzahlen sind, aber noch nicht durchgestrichen wurden.