Beim Heapsort Algorithmus wird das zu sortierende Array in einen Heap umgewandelt. Diese haben den Vorteil, dass sich mit ihnen sehr effizient das größte bzw. das kleinste Element ermitteln lassen, was beim Sortieren zu großen Performance-Vorteilen führen kann. Heapsort hat eine Laufzeitkomplexität von O(n·log n).
Was ist ein Heap?
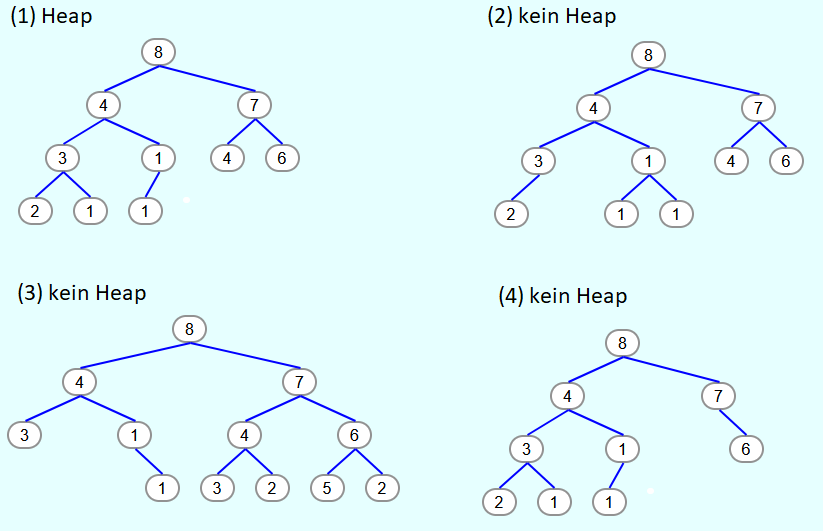
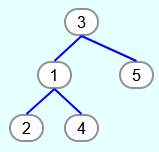
Ein Heap ist eine Datenstruktur, in welcher Elemente gespeichert werden können. Heaps sind spezielle Binärbäume, bei denen alle Ebenen, abgesehen eventuell von der untersten, komplett mit Elementen gefüllt sind. Wenn die unterste Ebene nicht vollständig mit Elementen gefüllt ist, ist die unterste Ebene von ganz links bis zu einer bestimmten Stelle gefüllt.
Bei dem ersten Baum handelt es sich um einen Heap, weil die obersten 3 Ebenen vollständig gefüllt sind und in der untersten Ebene die Elemente von ganz links und ohne Lücken aufgefüllt wurden.
Der zweite Baum ist kein Heap, weil in der untersten Ebene das zweite Element von links fehlt.
Baum 3 ist kein Heap, weil in der untersten Ebene die Elemente nicht von links aufgefüllt wurden.
Der vierte Baum ist kein Heap, weil in der dritten Ebene ein Element fehlt und somit nicht nur die unterste Ebene unvollständig ist.
Heapeigenschaft:
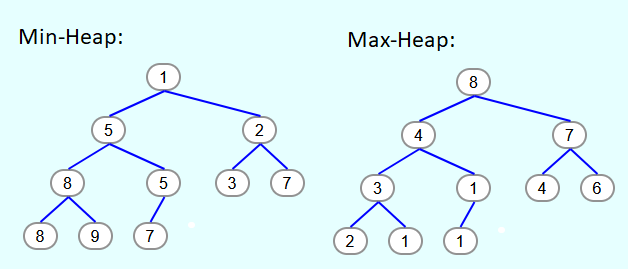
Man unterscheidet Min-Heaps und Max-Heaps. Bei Min-Heaps gilt für jedes Element, dass es kleiner oder gleich seinen Kindelementen ist und bei Max-Heaps sind alle Elemente größer oder gleich wie die Kindelemente. Insbesondere gibt es in einem Min-Heap kein Element, welches kleiner als das oberste Element ist und in einem Max-Heap gibt es kein Element, welches größer als das oberste Element ist.
Heaps und Arrays:
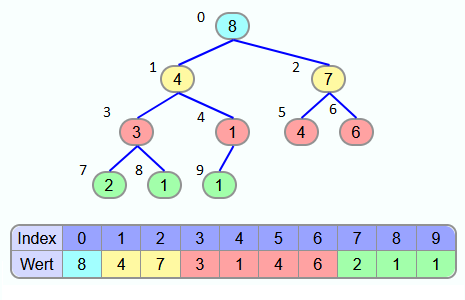
In der Praxis werden Heaps häufig nicht als Baumstruktur implementiert, sondern mit der Hilfe von einem Array. Die Baumstruktur dient als mentales Modell. Im Array enthält das Feld mit dem Index 0 den obersten Knoten von der Baumstruktur. In den darauffolgenden Feldern stehen die beiden Kindknoten des obersten Elements. In den darauffolgenden Feldern stehen die 4 Elemente aus der dritten Ebene von der Baumstruktur und danach von der vierten Ebene und so weiter. Die Elemente aus einer Ebene stehen immer in der Reihenfolge im Array, in der sie auch in der Ebene von der Baumstruktur vorkommen. Immer vom Element ganz links bis zum Element ganz rechts.
Index Kindknoten: Die Kindknoten von einem Element mit dem Index i stehen in den Feldern 2·i+1 und 2·i+2. Zum Beispiel sind die Kindknoten von dem Element mit dem Index 3 in den Feldern 2·3+1 = 7 und 2·3+2 = 8.
Index Elternknoten: Um den Index des Elternknotens von einem Element mit dem Index i zu berechnen, muss man (i-1)/2 berechnen und das Ergebnis abrunden.
Funktionsweise Heapsort
Im Folgenden soll ein Array aufsteigend mit dem Heapsort-Algorithmus sortiert werden und es wird ein Max-Heap verwendet. Das Array absteigend zu sortieren würde aber äquivalent durch die Verwendung eines Min-Heaps funktionieren.
Grundidee:
Zuerst wird das Array in einen Max-Heap umgewandelt, bei dem die Max-Heap-Eigenschaft (jeder Knoten ist größer oder gleich seinen Kindknoten) erfüllt ist. Wenn dies geschehen ist, befindet sich in der Wurzel das größte Element. Dieses Element wird mit dem letzten Element im Heap vertauscht und danach aus dem Heap entfernt. Da nun das Element in der Wurzel potentiell nicht mehr größer oder gleich den Kindknoten ist, muss die Heapeigenschaft wiederhergestellt werden. Wenn dies erledigt ist, enthält die Wurzel wieder das größte Element. Dieses wird wieder mit dem letzten Element im Heap vertauscht und aus dem Heap entfernt und danach wird wieder die Heapeigenschaft wiederhergestellt. Dies wird so lange gemacht, bis alle Elemente aus dem Heap entfernt wurden und sortiert im Ausgabearray stehen.
versickern-Methode:
Um dies zu erreichen wird eine Hilfsmethode "versickern()" benötigt. Sehr häufig wird diese auch "heapify()" genannt. Diese Methode erhält den Heap (als Array), den Index der Wurzel eines Teilbaums des Heaps, für den die Heapeigenschaft erfüllt werden soll und den Index vom letzten Element im Heap. Die Methode setzt voraus, dass für alle Nachfahren von der Wurzel des Teilbaums gilt, dass sie größer oder gleich den Kindknoten sind. Die Wurzel des Teilbaums darf aber vor dem Aufruf kleiner sein als ihre Kindknoten. Nach dem Aufruf soll für den gesamten Teilbaum die Max-Heapeigenschaft gelten.
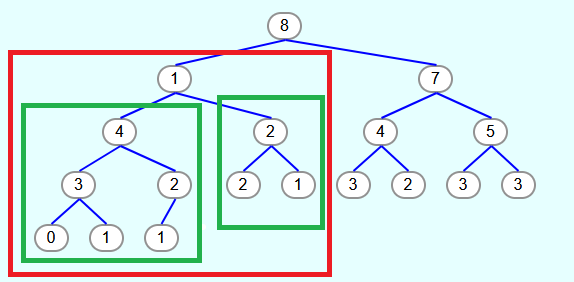
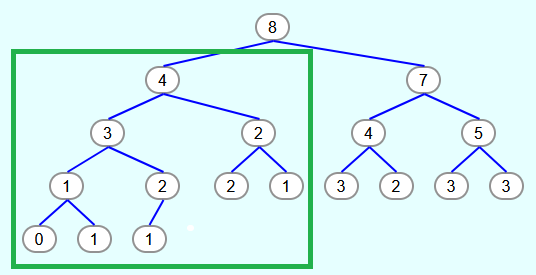
Als Beispiel wird beim folgenden Baum die versickern-Methode mit dem Index 1 aufgerufen.
Es soll also der rot umrahmte Teilbaum zu einem Max-Heap umgewandelt werden. Die Voraussetzung ist, dass für die Teilbäume links und rechts vom Element mit dem Index 1 (grün umrahmt) die Max-Heapeigenschaft gilt. Das ist der Fall. Das Element mit dem Index 1 muss aber nicht zwingend größer oder gleich sein wie die Kindknoten.
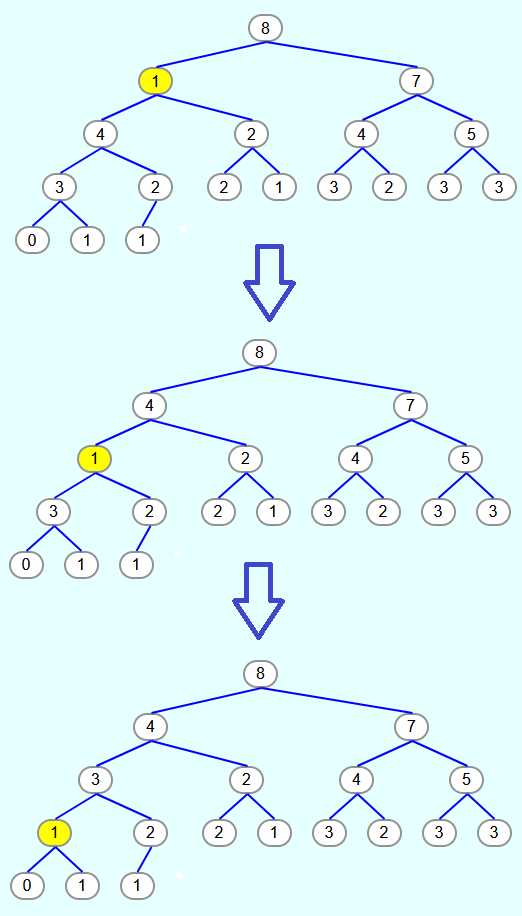
Nach dem Aufruf der versickern-Methode soll der Heap wie folgt aussehen:
Dies wird erreicht, indem das Element, welches ursprünglich in der Wurzel vom Teilbaum stand (in diesem Fall die 1) so lange mit seinem größten Kindknoten vertauscht wird, bis es keinen Kindknoten mehr hat, welcher größer als das zu versickernde Element selber ist.
Im obigen Beispiel hat der Knoten mit dem Index und Wert 1 Kindknoten mit den Werten 4 und 2. Somit wird die 1 mit der 4 vertauscht. Dann hat die 1 Kindknoten mit den Werten 3 und 2. Also wird das Element mit der 3 vertauscht. Danach haben die Kindknoten die Werte 0 und 1. Da keiner der beiden Werte größer als 1 ist, ist die 1 nun an der richtigen Stelle.
Vorgehen:
Heap aufbauen: Zuerst wird der Heap aufgebaut. Dafür wird das Array so umsortiert, dass die Heap-Eigenschaft erfüllt ist (alle Knoten sind größer oder gleich groß wie groß wie Kindknoten). Dazu wird die oben eingeführte versickern-Methode verwendet. Es wird für jeden Knoten, welcher mindestens ein Kindknoten hat, die versickern-Methode aufgerufen. Aufgrund von der Vorbedingung der versickern-Methode ist es wichtig, dass mit dem letzten Knoten begonnen wird und sich dann Ebene um Ebene weiter nach oben durchgearbeitet wird, bis als letztes für die Wurzel die versickern-Methode aufgerufen wird. Um den letzten Knoten, welcher mindestens einen Kindknoten hat, zu ermitteln, wird die Länge vom Array durch 2 geteilt und das Ergebnis wird abgerundet und um 1 verringert (abrunden(A.länge/2)-1).
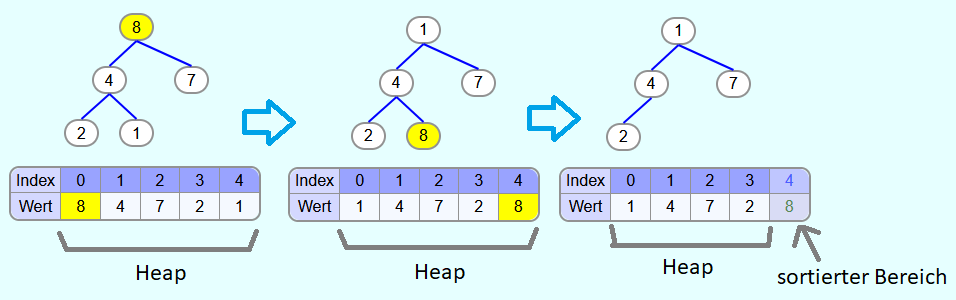
größtes Element aus Heap entfernen: Nachdem der Heap aufgebaut wurde befindet sich das größte Element in der Wurzel. Dieses soll am Ende vom Ausgabearray eingefügt und aus dem Heap gelöscht werden. Anstatt dass dafür ein extra Array erstellt werden muss, kann dafür auch das Array genutzt werden, welches auch für den Heap genutzt wird. Im vorderen Teil vom Array sind die Elemente vom Heap abgespeichert und im hinteren Teil entsteht das sortierte Array. In jeder Iteration der zweiten Schleife wird zuerst oberste (also das größte) Element mit dem letzten Element vom Heap vertauscht. Danach wird es nicht mehr als zum Heap zugehörig angesehen, sondern als zum sortierten Bereich gehörend, betrachtet.
Heapeigenschaft wiederherstellen: Nachdem das größte Element und das letzte Element im Heap vertauscht wurden und das größte Element aus dem Heap entfernt wurde, ist das neue Wurzelelement potentiell kleiner als mindestens eines der Kindknoten. Um die Max-Heapeigenschaft wiederherzustellen muss die versickern-Methode mit dem Index der Wurzel (also 0) aufgerufen werden. Da das Feld mit dem Index j nun nicht mehr zum Heap gehört, wird der Methode j-1 als Index des letzten Heapelements übergeben.
Die Schritte "größtes Element aus Heap entfernen" und "Heapeigenschaft wiederherstellen" werden so lange abwechselnd wiederholt, bis der Heap nur noch 1 Element enthält. Da ein einzelnes Element automatisch sortiert ist, ist dann das gesamte Array sortiert.
kleines Beispiel
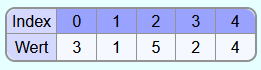
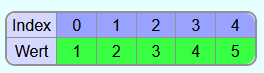
Es soll das folgende Array mit dem Heapsort-Algorithmus sortiert werden:
Als Heap dargestellt sieht es wie folgt aus:
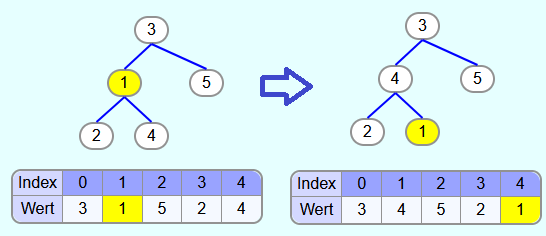
Initialisierung - Heap aufbauen:
Es gibt nur 2 Knoten mit Kindknoten. Zuerst wird versickern-Methode mit dem Index 1 aufgerufen. Da die 1 größere Kindknoten hat, wird sie mit dem größten Kindknoten (also der 4) vertauscht.
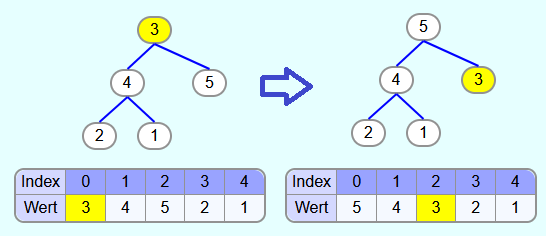
Danach wird die versickern-Methode mit dem Index 0 aufgerufen. Da die 3 kleiner ist als die 5 und da 5 größer ist als 4, wird die 3 mit der 5 vertauscht.
Die Max-Heapeigenschaft ist nun erfüllt.
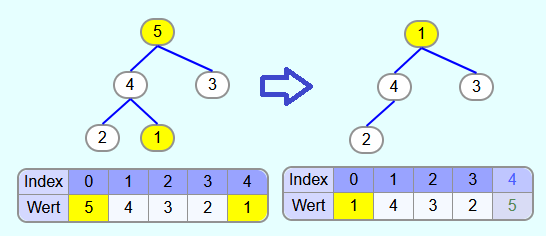
Iteration 1:
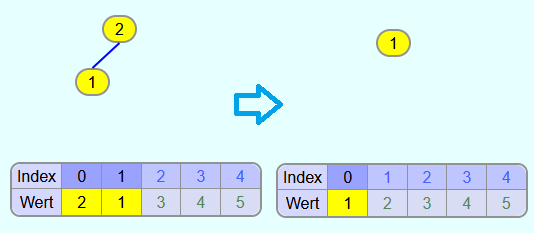
Die Wurzel wird mit dem letzten Element vertauscht und aus dem Heap entfernt.
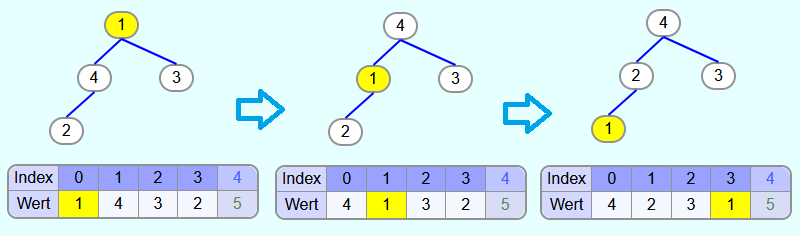
Die 1 verletzt die Heapeigenschaft. Um diese wiederherzustellen, muss die 1 "versickert" werden. Die 4 ist der größte Kindknoten und somit wird die 1 mit der 4 getauscht. Danach wird die 1 mit der 2 getauscht.
Iteration 2:
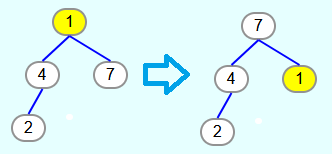
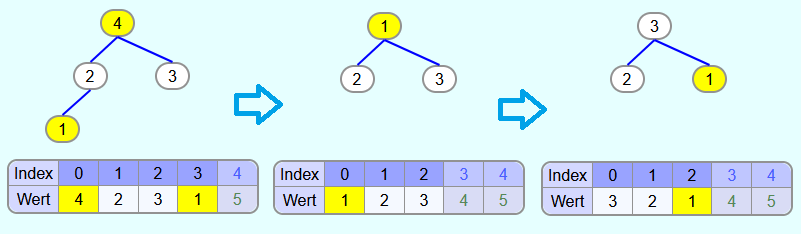
Als nächstes wird die 4 mit dem letzten Element vertauscht und aus dem Heap entfernt. Danach wird die 1 in der versickern-Methode mit dem größten Kindknoten (also der 3) vertauscht.
Iteration 3:
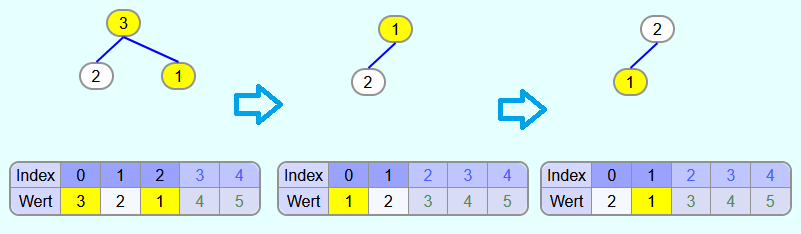
Iteration 4:
Ergebnis:
Da sich nur noch 1 Element im Heap befindet, ist dieses automatisch an der richtigen Stelle und das Array ist sortiert.