Insertionsort ist ein Algorithmus zum Sortieren von Listen und Arrays. Das Sortierverfahren ist für Arrays, die schon zu einem großen Teil vorsortiert sind, sehr effizient.
Funktionsweise
Grundidee:
Das Array ist unterteilt in einen sortierten Teil gefolgt von einem unsortierten Teil. Anders als zum Beispiel bei Selection Sort oder Bubble Sort haben die Elemente aus dem sortierten Bereich aber potentiell noch nicht ihre finale Position erreicht. Beim Insertion-Sort-Algorithmus wird in jeder Iteration das vorderste Element aus dem unsortierten Bereich in den sortierten Bereich einsortiert. Dies wird erreicht, indem die Position gesucht wird, an welcher das Element einsortiert werden soll, alle größeren Elemente um 1 Feld nach rechts verschoben werden, damit Platz für das einzufügende Element ist, und das einzufügende Element danach an der gefunden Stelle eingefügt wird.
Zum Beispiel soll vor einem Iterationsschritt das Array wie folgt aussehen:
Die bläulichen Felder sind der sortierte Teil vom Array und die weißen Felder sind der unsortierte Teil. Als nächstes soll das vorderste Element aus dem unsortierten Bereich in den sortierten Bereich einsortiert werden. Das ist die 6. Die 6 gehört zwischen die 5 und die 7. Damit die 6 einsortiert werden kann, müssen zuerst noch die 7 und die 8 jeweils 1 Feld weiter nach rechts verschoben werden.
Nach dem Iterationsschritt sieht das Array wie folgt aus:
Pseudocode:
Vorgehen:
Vor jeder Iteration der äußeren Schleife besteht der sortierte Bereich aus den Elementen mit den Indizes 0 bis i-1 und das Element an der Stelle i soll in diesen Teilbereich einsortiert werden. Da ein einelementiges Teilarray automatisch sortiert ist, kann das Array mit i = 1 anstatt von i = 0 beginnen.
j ist der Index des Feldes, für welches gerade überprüft wird, ob es sich um ein Feld handelt, in welches das einzufügende Element eingefügt werden kann, sodass der sortierte Teil hinterher weiterhin sortiert ist. Zu Beginn wird j auf den Index vom ersten Element hinter dem sortierten Bereich gesetzt. Also auf das Feld des Elementes, welches einsortiert werden soll.
Da das Feld mit dem Element, welches eingefügt werden soll, in der inneren Schleife überschrieben werden kann, wird der einzufügende Wert in der Variable "einzufügen" zwischengespeichert.
Mit der inneren Schleife wird nach dem Index gesucht, bei dem das Element eingefügt werden soll. Dafür wird sich immer das Element links von der Position j angesehen. Wenn das Element mit dem Index j-1 größer als das Element ist, welches eingefügt werden soll, dann wird es nach rechts verschoben, um Platz für das neu einzufügende Element zu schaffen. Danach wird j um 1 weiter nach links gesetzt. Dies wird so lange gemacht, bis j entweder den Anfang vom Array erreicht hat oder bis das Element im Feld vor j kleiner als das einzufügende Element ist. Wenn dies der Fall ist, ist j die Position, an der das Element eingefügt wird.
Beispiel
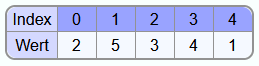
Als Beispiel soll das folgende Array sortiert werden:
Iteration 1:
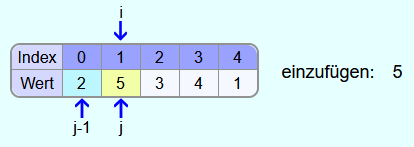
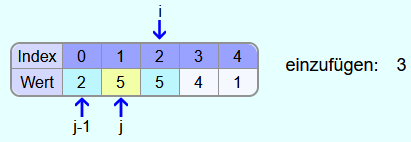
Vor der ersten Iteration befindet sich nur das erste Element, also die 2, im sortierten Bereich. Die 5 soll einsortiert werden. Also wird j auf den Index 1 gesetzt und die 5 wird zwischengespeichert.
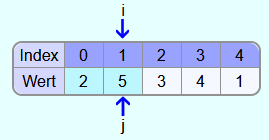
Jetzt wird die 2 mit der 5 verglichen. Da die 5 größer ist, ist die 5 schon an der richtigen Position.
Iteration 2:
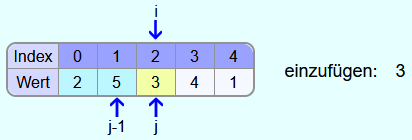
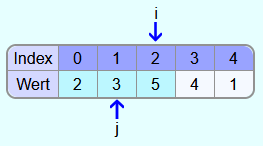
Als nächsten soll die 3 in den sortierten Bereich eingefügt werden.
Diesmal ist das Element an der Stelle j-1 größer als das einzufügende Element und somit muss die 5 in das Feld an der Stelle j kopiert werden. Danach wird j ein Feld weiter nach links gesetzt.
Wie auf dem Bild zu sehen ist, steht die 5 jetzt sowohl im Feld mit dem Index 1 als auch im Feld mit dem Index 2. Das ist aber nicht schlimm, weil die 5 im Feld mit dem Index 1 entweder durch die Zahl im Feld mit dem Index 0 oder durch die Zahl, die eingefügt werden soll, überschrieben werden wird.
Da 2 nicht größer ist als 3, wird die 3 in das Feld mit dem Index 1 eingetragen.
Iteration 3:
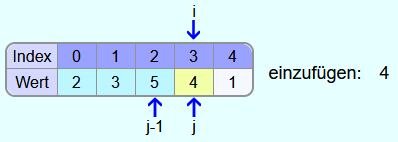
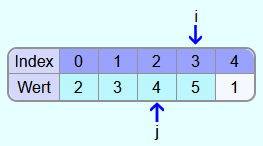
Als nächstes soll die 4 eingefügt werden.
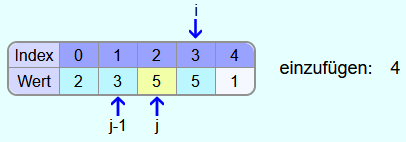
Die 5 ist größer als die 4. Somit muss die 5 wieder ein Feld weiter nach rechts kopiert werden und j wird um 1 verringert.
Die 3 ist nicht größer als die 4 und somit muss die 4 in das Feld mit dem Index 2 eingetragen werden.
Iteration 4:
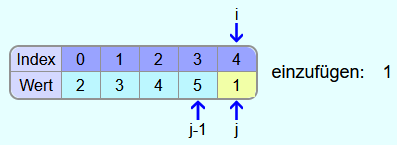
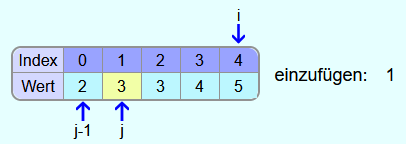
Als letzte Zahl soll die 1 in den sortierten Bereich eingefügt werden.
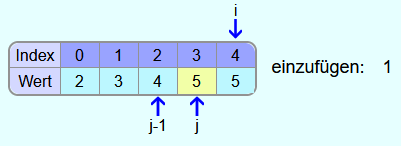
Die 5 ist größer als die 1 und somit wird die 5 nochmal ein Feld weiter nach rechts kopiert.
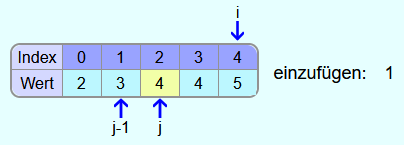
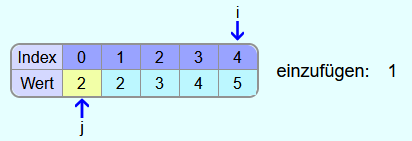
Die 4, die 3 und die 2 sind auch alle größer als 1 und somit werden sie ebenfalls alle nacheinander ein Feld weiter nach rechts kopiert.
Jetzt gibt es links von j kein Feld mehr und somit wird die 1 in das Feld ganz links eingetragen.
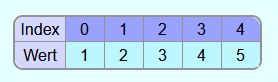
Das Array ist jetzt sortiert.
Laufzeitkomplexität
Angenommen das Array ist falsch herum sortiert. Dann muss in jeder Iteration vom Insertionsort-Algorithmus einmal der gesamte sortierte Bereich durchlaufen werden. Dies führt zu einer quadratischen Laufzeitkomplexität.
Ist hingegen das Array richtig herum sortiert, wird für jedes Element schon beim ersten Versuch die richtige Stelle zum Einfügen gefunden, was dazu führt, dass die Laufzeitkomplexität in diesem Fall linear ist.
Im Durchschnitt ist die Laufzeitkomplexität quadratisch.
Der Algorithmus ist für Arrays, bei denen ein Großteil der Elemente schon sortiert ist, sehr effizient.