Der Algorithmus von Kruskal erhält einen Graphen G=(V, E) einen erstellt von diesem einen minimalen Spannbaum G'=(V, E').
Was ist ein minimaler Spannbaum?
Ein Spannbaum ist ein Teilgraph eines ungerichteten und zusammenhängenden Graphen G. Für den Teilgraph müssen die folgenden Bedingungen gelten:
- Alle Knoten, die im Graphen G enthalten sind, sind auch im Teilgraph enthalten.
- Der Teilgraph ist zusammenhängend und frei von Zyklen.
- Die Menge der Kanten des Teilgraphen ist eine Teilmenge der Kantenmenge von G.
Ein Spannbaum G' ist ein minimaler Spannbaum von G, wenn es keinen Spannbaum von G gibt, dessen Summe aller Kantengewichte kleiner ist als die Summe aller Kantengewichte von G'.
Beispiel zu Spannbäumen:
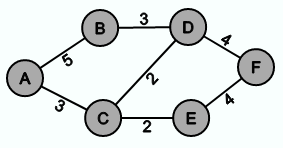
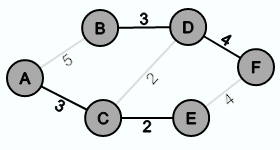
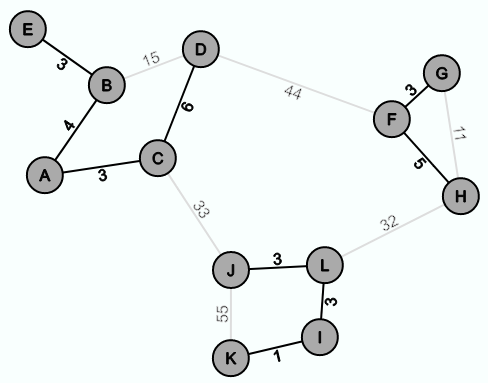
Als Beispiel soll der Graph G wie folgt aussehen:
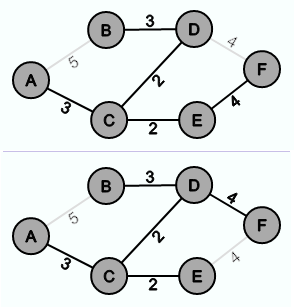
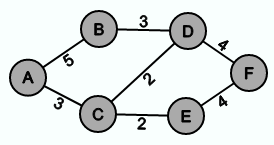
Die folgenden beiden Graphen sind beide minimale Spannbäume von G, weil sie beide Spannbäume von G sind und es keinen Spannbaum von G gibt, dessen Summe der Kantengewichte kleiner als 14 sind.
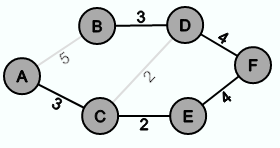
Der folgende Graph ist ein Spannbaum von G, weil der Graph frei von Zyklen und zusammenhängend ist und weil alle Knoten aus G auch in diesem Graphen enthalten sind. Aber die Summe der Kantengewichte beträgt 16 und es 2 Spannbäume, bei denen die Summe der Kantengewichte 14 beträgt. Somit ist der folgende Graph zwar ein Spannbaum von G, aber kein minimaler:
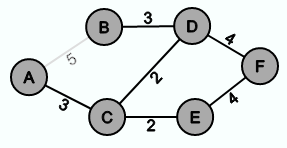
Der folgende Graph enthält einen Zyklus und ist somit kein Spannbaum.
Der folgende Graph ist nicht zusammenhängend und ist somit kein Spannbaum.
Funktionsweise von Kruskals Algorithmus
Pseudocode
Eingabe:
Kruskals Algorithmus erhält einen ungerichteten und zusammenhängenden Graphen G=(V, E), wobei V die Menge der Knoten und E die Menge der Kanten ist.
Wichtige Werte und Mengen:
E': die Menge der Kanten des sich entwickelnden minimalen Spannbaums
Q: die Menge der Kanten, für die sich noch nicht entschieden wurde, ob sie in E' eingefügt werden sollen oder nicht
e: die Kante, für die sich gerade entschieden wird, ob sie in E' eingefügt werden soll
Ziel:
Nach der Ausführung vom Algorithmus von Kruskal bildet (V, E') einen minimalen Spannbaum von G
Initialisierung:
Zu Beginn befinden sich noch keine Kanten in der Kantenmenge E'. Alle Kanten aus E werden in Q eingefügt und Q wird aufsteigend nach den Kantengewichten sortiert.
Schleife:
In jeder Iteration wird die Kante mit dem kleinsten Kantengewicht aus Q entfernt. Wenn sich diese in E' einfügen lässt, ohne dass dadurch im sich entwickelnden minimalen Spannbaum ein Zyklus entsteht, wird die Kante in E' eingefügt.
Beispiel zum Kruskal-Algorithmus:
Als Beispiel soll ein minimaler Spannbaum des Graphen aus dem vorherigen Kapitel mit dem Kruskal-Algorithmus erstellt werden.
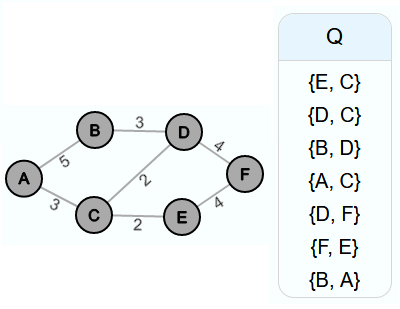
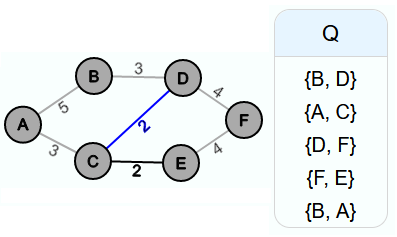
Die Kantenmenge des neuen Graphen E' ist am Anfang noch leer. Alle Kanten des Beispielgraphen werden in Q eingefügt und Q wird nach den Kantengewichten aufsteigend sortiert.
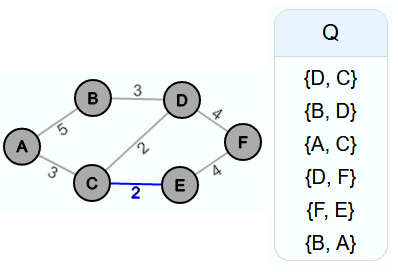
In der ersten Iteration wird die Kante {E, C} aus Q entfernt. Da sich kein Zyklus bildet, wenn man sie in den neuen Graphen einfügt, wird sie in E' eingefügt.
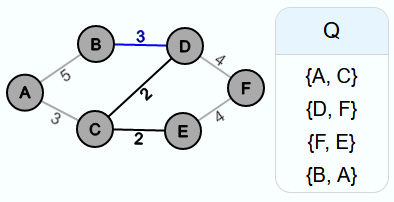
Genau so verfährt man auch in der zweiten Iteration. Es wird die Kante {D, C}, also die Kante mit dem kleinsten Kantengewicht, aus Q entfernt. Und da auch diese in E' eingefügt werden kann, ohne dass sich ein Zyklus bildet, wird sie in E' eingefügt.
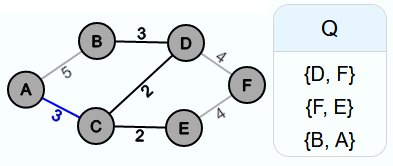
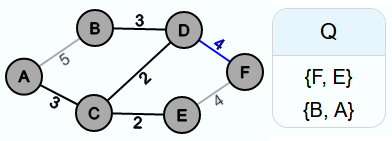
Auch in den nächsten 3 Iterationen bildet sich kein Zyklus und somit werden die Kanten {B, D}, {A, C} und {D, F} in E' eingefügt.
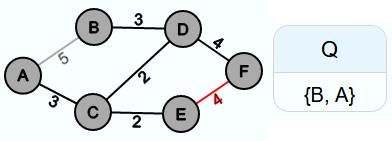
In der sechsten Iteration würde es zu einem Zyklus kommen, wenn {F, E} in E' eingefügt werden würde. Also wird sie nicht in E' eingefügt, nachdem sie aus Q entfernt wurde.
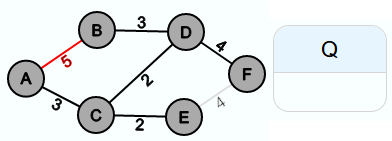
Auch in der siebten Iteration würde ein Zyklus entstehen, wenn man {B, A} in E' einfügen würde. Also wird auch {B, A} nicht in E' eingefügt.
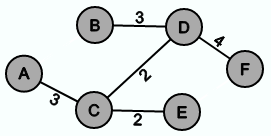
Der entwickelte minimale Spannbaum sieht also wie folgt aus:
Auf Zyklen prüfen
Im Prinzip funktioniert der Algorithmus also sehr einfach. Bisher wurde aber noch außer Acht gelassen, wie die Prüfung auf Zyklen funktioniert. Dafür wird eine sogenannte "Union-Find-Struktur" verwendet.
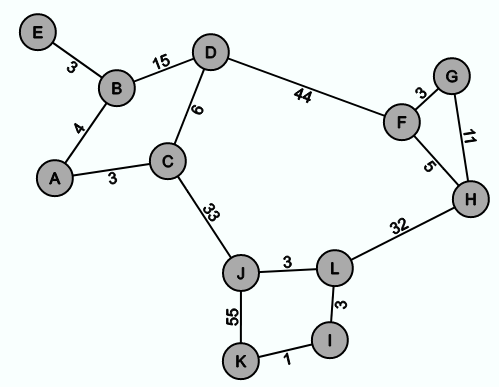
Angenommen es soll für den folgenden Graph ein minimaler Spannbaum ermittelt werden:
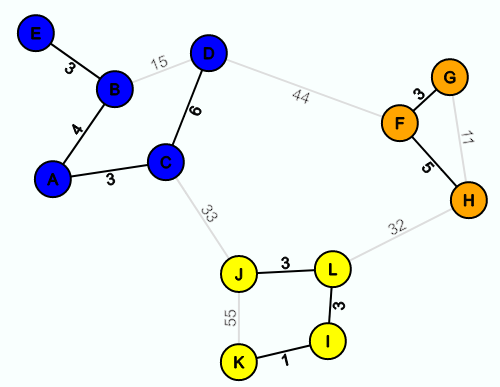
Nach 9 Iterationen vom Kruskal-Algorithmus sieht der Graph wie folgt aus, wobei die grauen Kanten die Kanten sind, für die sich noch nicht entschieden wurde, ob sie in E' eingefügt werden sollen oder nicht:
Jetzt nehmen wir mal an, dass genau die Knoten zu einer gemeinsamen Gruppe mit einer gemeinsamen Farbe gehören, die direkt oder indirekt miteinander durch Kanten in E' verbunden sind.
Wie entscheidet man nun für eine Kante, ob sie in E' eingefügt werden soll? Wenn die beiden zur Kante gehörenden Knoten die gleiche Farbe haben, dann bedeutet das, dass es schon einen Pfad zwischen den beiden Knoten im Graphen (V, E') gibt. Wenn man die Kante einfügen würde, wären die beiden Knoten sowohl über den schon vorhandenen Pfad als auch über die neue Kante miteinander verbunden und damit wäre ein Zyklus entstanden.
Wenn die beiden Knoten unterschiedliche Farben haben, dann bedeutet das, dass es bisher noch keinen Pfad zwischen ihnen gibt und somit würde es zu keinem Zyklus führen, wenn man die Kante in E' einfügen würde, weil die neue Kante die einzige Verbindung zwischen den beiden Knoten wäre.
Für den Algorithmus bedeutet das, dass man die Kante genau dann einfügt, wenn beide Knoten die unterschiedliche Farben haben. Damit der Algorithmus auch in zukünftigen Iterationen zuverlässig funktioniert, müssen die beiden Gruppen, der beiden durch die neue Kante verbundenen Knoten, zu einer Gruppe zusammengefasst werden.
In der Praxis werden den Gruppen natürlich keine Farben zugeordnet. Stattdessen gibt es für jede Gruppe einen Knoten, der diese Gruppe repräsentiert. Das zusammenführen von 2 Gruppen wäre aber bei sehr großen Gruppen mit einem hohen Aufwand verbunden, wenn für eine der beiden Gruppen jedem Knoten einzeln ein neuer Repräsentant zugewiesen werden würde. Deshalb wird eine baumähnliche Struktur eingeführt, bei der der Knoten, der die Gruppe repräsentiert, die Wurzel ist. Für jeden Knoten v∈V wird eine Variable vorgänger[v] eingeführt. Wenn v eine Wurzel ist, wird vorgänger[v] der symbolische Wert null zugewiesen. Ansonsten ist vorgänger[v] ein Knoten auf dem Pfad zwischen v und der Wurzel, wobei vorgänger[v] auch die Wurzel sein darf, aber nicht v selber. Somit ist sichergestellt, dass für jeden Knoten die Wurzel über die Vorgängerknoten erreicht werden kann und dass die Wurzel sich selber als Wurzel erkennen kann.
Bei Union-Find-Strukturen gibt es 2 wichtige Methoden: finden (find) und vereinigen (union)
finden(v) liefert die Wurzel des Baumes zurück, in dem sich v befindet.
vereinigen(u, v) führt führt den Baum von u und den Baum von v zu einem Baum zusammen. Dafür wird die Vorgängerreferenz von der einen Wurzel auf die Wurzel vom anderen Knoten gesetzt.
Am besten lässt sich dies anhand von einem Beispiel zeigen. Eingabegraph ist wieder der Graph von weiter oben:
In den folgenden Abbildungen bedeutet ein Pfeil vom Knoten u zum Knoten v, dass vorgänger[u] == v gilt. Der Verweis von der Wurzel auf null wird nicht abgebildet.
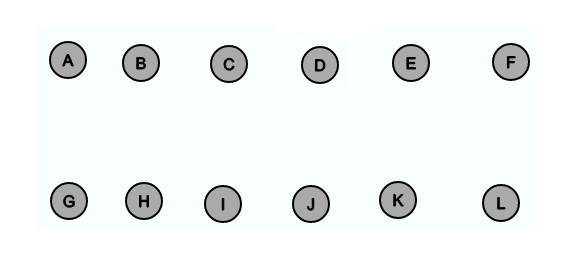
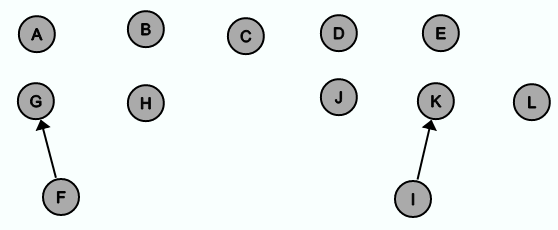
Zu Beginn von Kruskals Algorithmus ist E' noch leer und deshalb befindet sich jeder Knoten in einer eigenen Gruppe mit sich selber als Wurzel.
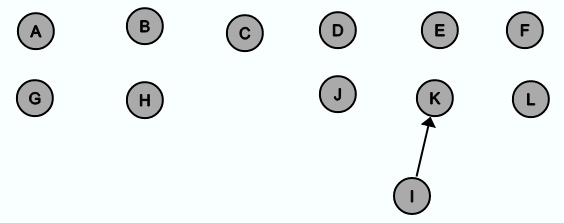
In der ersten Iteration wird geprüft, ob die Kante {K, I} in E' eingefügt werden soll. Da finden(K) und finden(I) unterschiedliche Knoten zurück liefern, wird zum einen die Kante {K, I} in E' eingefügt und zum anderen wird entweder der Vorgänger von K auf I gesetzt oder anders herum. In diesem Fall wird K der Vorgänger von I.
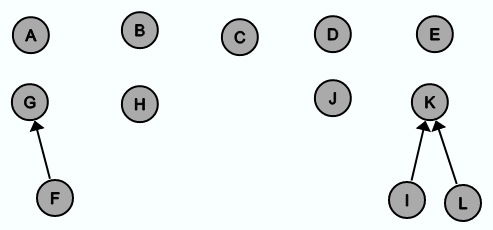
Wenn als nächstes die Kante {F, G} eingefügt werden soll, werden wieder finden(F) und finden(G) miteinander verglichen und da finden(F) != finden(G) gilt, wird die Kante in E' eingefügt und die beiden Bäume werden in der Union-Find-Struktur vereinigt.
In der dritten Iteration wird die Kante {I, L} in E' eingefügt, weil finden(I) = K != L = finden(L) gilt. Es ist sinnvoll die Bäume möglichst flach zu halten. Da der Baum mit der Wurzel L eine geringere Höhe hat als der Baum mit der Wurzel K, wird L an K angehängt.
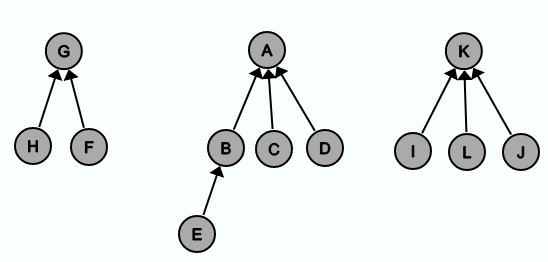
Und so geht es weiter. Nach 9 Iterationen sieht der sich entwickelnde Spannbaum wie folgt aus:
Und die Union-Find-Struktur:
Als nächstes wird geprüft, ob die Kante {G, H} in E' eingefügt werden soll. Da finden(G) = G == G = finden(H) gilt, wird die Kante nicht in E' eingefügt und die Union-Find-Struktur wird auch nicht geändert. Das Gleiche passiert beim Versuch {B, D} in E' einzufügen.
Bei der Kante {L, H} kommen aber wieder unterschiedliche Wurzeln heraus und deshalb kann die Kante wieder in E' eingefügt werden und die Bäume in der Union-Find-Struktur werden wieder zusammengelegt.
Auch die Kante {C, J} kann in E' eingefügt werden und die Union-Find-Struktur wird wieder angepasst.
D und F haben das gleiche Wurzelelement und das Gleiche gilt für J und K. Deshalb werden {D, F} und {J, K} nicht in den minimalen Spannbaum mit aufgenommen.
Pseudocode Kruskal mit Union-Find
Jetzt soll der Pseudocode von oben um Code für den Union-Find-Algorithmus erweitert werden:
Wenn es sich um einen Wurzelknoten handelt, wird der Knoten selber zurück gegeben. Ansonsten wird finden mit dem Vorgängerknoten aufgerufen.
Es wurde für jeden Knoten v∈V eine Variable rang[v] eingeführt, die angibt wie hoch der Baum ist. Damit beim Aufruf von finden nicht zu viele Knoten durchlaufen werden müssen, sollte immer der niedrigere Baum in den höheren eingefügt werden. Die Höhe des Baumes, an dessen Wurzeln der andere Baum angehängt wird verändert sich nur, wenn beide Bäume gleich hoch sind.
Union-Find komprimieren
Auch wenn man immer den kleineren Baum an die Wurzel vom größeren Baum hängt, um die Bäume flacher zu halten, können die Bäume bei sehr großen Graphen ziemlich hoch werden. Beim Aufruf von finden muss dann jedes mal die gesamte Kette durchgegangen werden. Das ist natürlich mit sehr viel Aufwand verbunden. Dieser Aufwand kann deutlich reduziert werden, wenn die Vorgängerreferenz direkt auf die Wurzel zeigen würde. Wie schon weiter oben beschrieben sollte aber auch nicht bei jedem Vereinigen von 2 Bäumen jedem Knoten des einen Baumes die Wurzel des anderen Baumes einzeln als Vorgänger zugewiesen werden. Ein guter Kompromiss ist, dass man bei jedem Aufruf der finden-Methode, bei dem die Methode nicht auf das Wurzelelement angewendet wurde, der Vorgänger auf den Wurzelknoten gesetzt wird, der sowieso zurückgeliefert wird.
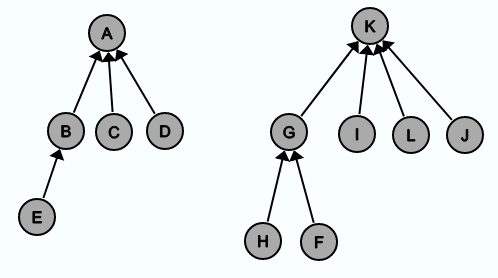
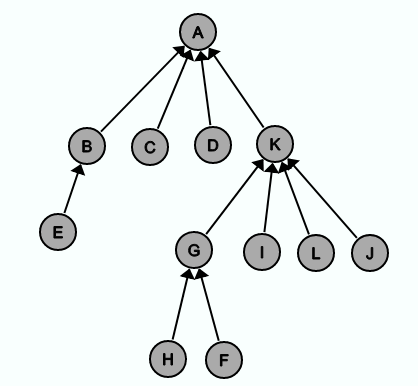
Als Beispiel soll finden(H) bei dem folgenden Baum aufgerufen werden:
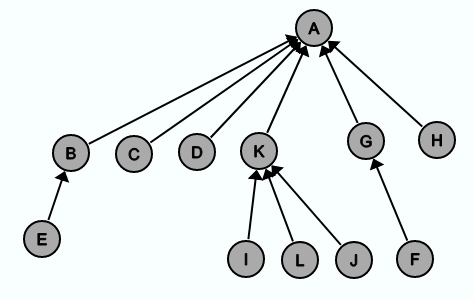
Beim Aufruf von finden(H) werden insgesamt 4 Knoten durchlaufen. Wenn jeder durchlaufene Knoten (außer der Wurzel) direkt an die Wurzel gehängt wird, sieht der Baum hinterher wie folgt aus:
Wenn finden(H) noch einmal aufgerufen werden würde, müssten nur noch 2 Knoten durchlaufen werden.
Die finden-Methode kann dafür wie folgt abgewandelt werden: