Mergesort ist ein effizienter Sortieralgorithmus, bei dem die Liste bzw. das Array in immer kleinere Listen oder Arrays aufgeteilt wird, die später sortiert wieder zusammengesetzt werden.
Funktionsweise
Grundidee:
Beim Mergesort-Algorithmus wird die Liste, die sortiert werden soll, zuerst in 2 neue Listen aufgeteilt. Diese Listen werden rekursiv mit Mergesort sortiert. Danach werden die beiden sortierten Listen wieder zu einer Liste zusammengefügt.
Pseudocode:
Vorgehen:
Wenn die Liste, mit der Mergesort aufgerufen wird, weniger als 2 Elemente enthält, ist die Liste automatisch sortiert. In diesem Fall muss an der Liste nichts verändert werden.
Wenn die Liste mehr als ein Element enthält, wird die Liste in eine linke und eine rechte Liste aufgeteilt. In beide neuen Listen sollte nach Möglichkeit die gleiche Anzahl an Elementen eingefügt werden. Bei ungerader Anzahl an Elementen wird in eine der beiden neuen Listen 1 Element mehr eingefügt, als in die andere.
Danach wird Mergesort rekursiv auf die beiden neuen Listen angewendet, sodass die beiden Listen nach diesen Aufrufen jeweils sortiert sind.
Dann müssen die beiden sortierten Listen miteinander verschmolzen werden. Dafür wird sich immer das vorderste Element aus beiden Listen angesehen. Wenn das vorderste Element aus der linken Liste kleiner ist als das vorderste Element aus der rechten Liste, dann wird das vorderste Element aus der linken Liste aus der Liste entfernt und hinten in die Ausgabeliste eingefügt. Und wenn das erste Element aus der rechten Liste kleiner ist, als das erste Element aus der linken, dann wird das Element aus der rechten Liste entfernt und hinten an die Ausgabeliste angehängt. Dies wird so lange wiederholt, bis eine der beiden Listen leer ist. Wenn dies der Fall ist, dann werden die restlichen Elemente aus der noch nicht leeren Liste am Ende der Ausgabeliste eingefügt. Wenn dies erledigt ist, dann ist die Ausgabeliste sortiert.
Beispiel
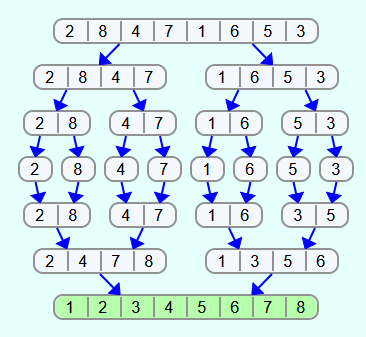
Als Beispiel soll die folgende Liste sortiert werden:
Zuerst wird die Liste in 2 Listen aufgeteilt.
Danach wird der Mergesort-Algorithmus auf die beiden Listen angewendet. Dadurch erhält man 2 sortierte Listen.
Diese Listen sollen zu einer Liste zusammengefügt werden.
Dafür werden immer die ersten beiden Elemente der 2 Listen verglichen und die kleinere Zahl wird aus der Liste entfernt und in die Ergebnisliste hinten eingefügt. Da 1 kleiner als 2 ist, wird die 1 aus Liste 2 entfernt und in die noch leere Ergebnisliste eingefügt.
Es werden wieder die ersten beiden Elemente verglichen und da 2 kleiner als 3 ist, wird die 2 aus Liste 1 entfernt und an die Ergebnisliste angehängt.
Und so geht es weiter, bis eine der beiden Listen leer ist.
Liste 2 ist nun leer. Das heißt, dass die beiden verbliebenden Elemente aus Liste 1 in die Ergebnisliste eingefügt werden können, ohne dass sie mit einem Element aus Liste 2 verglichen werden müssen.
Die Liste ist nun sortiert.
Im Beispiel wurde nur ein Aufruf von Mergesort durchgegangen, aber mit den beiden Listen, die in der "Teilen-Phase" erstellt werden und auf die Mergesort rekursiv angewendet wird, wird vom Prinzip her genau gleich verfahren. Die Listen werden so lange in immer kleinere Listen aufgespalten, bis die Listen nur noch aus einem Element bestehen und danach wieder zu sortierten Listen zusammengesetzt.