Der Algorithmus von Prim erhält einen Graphen G=(V, E) und erstellt von diesem einen minimalen Spannbaum G'=(V, E').
Was ist ein minimaler Spannbaum?
Angenommen G=(V,E) ist ein ungerichteter und zusammenhängender Graph. G' ist ein Spannbaum, wenn:
- G' genau die Knoten enthält, die auch im Graphen G enthalten sind
- G' nur Kanten enthält, die auch in G enthalten sind
- G' zusammenhängend und frei von Zyklen ist
Wenn es keinen Spannbaum von G gibt, bei dem die Summe der Kantengewichte kleiner ist als die Summe der Kantengewichte von G', dann ist G' ein minimaler Spannbaum von G.
Beispiel:
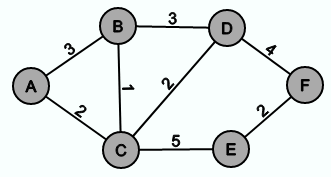
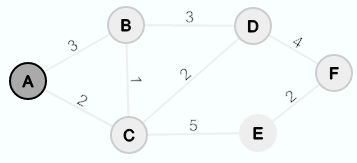
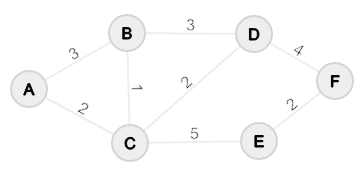
Angenommen der Graph sieht wie folgt aus:
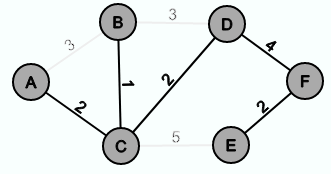
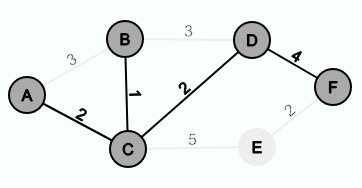
Ein minimaler Spannbaum sieht in diesem Fall wie folgt aus:
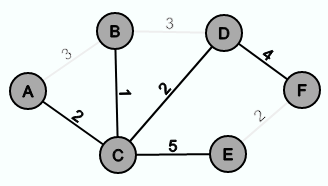
Der folgende Graph ist zwar ein Spannbaum des Beispielgraphen, aber da die Summe aller Kantengewichte 14 beträgt und es einen Spannbaum gibt, bei dem die Summe der Kantengewichte 11 ist, handelt es sich nicht um einen minimalen Spannbaum.
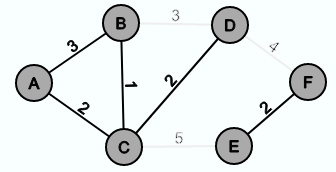
Der folgende Graph ist ist kein Spannbaum, weil er einen Zyklus enthält und nicht zusammenhängend ist:
Grundprinzip
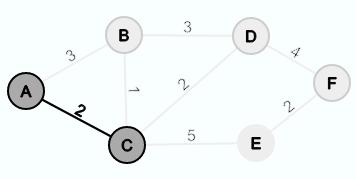
Als Beispiel soll wieder der Graph aus dem obigen Kapitel dienen. Man wählt zuerst einen Knoten aus G als Startknoten und fügt diesen in G' ein.
In jeder Iteration wählt man die Kante mit dem kleinsten Gewicht aus, die einen Knoten im neuen Graphen G' und einen Knoten, der sich noch nicht in G' befindet, miteinander verbindet und fügt sowohl die Kante als auch den Knoten, der sich noch nicht in G' befindet, in G' ein.
Es kann sich also zwischen der Kante {A,B} und der Kante {A,C} entschieden werden. Da die Kante {A,C} das kleinere Gewicht hat, werden der Knoten C und die Kante {A,C} in G' eingefügt.
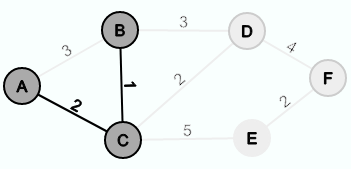
Als nächstes kann man sich zwischen den Kanten {A,B}, {C,B}, {A,B}, {C,D} und {C,E} entscheiden. Da die Kante {C,B} das kleinste Gewicht hat, wählt man diese.
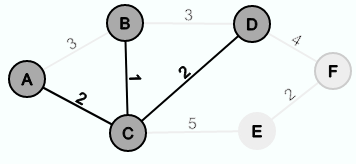
Als nächstes kann man sich zwischen {B,D}, {C,D} und {C,E} entscheiden und man wählt {C,D}.
Danach wählt man {D,F}.
Und als Letztes {F,E}.
Im Prinzip funktioniert der Algorithmus von Prim so wie in diesem Kapitel beschrieben, aber die obige Beschreibung war etwas vereinfachend.
Funktionsweise
Pseudocode
Eingabe:
Der Prim-Algorithmus erhält einen ungerichteten und zyklusfreien Graphen G=(V,E,start), wobei V die Menge der Knoten, E die Menge der Kanten und start der Startknoten ist.
Wichtige Werte und Mengen:
Q: Es wird eine Menge von Knoten Q benötigt. Diese enthält die Knoten, die noch nicht zum Spannbaum hinzugefügt wurden. Es bietet sich an dafür eine Prioritätswarteschlange (priority queue) zu verwenden.
abstand[v]: Für jeden Knoten v∈V wird der Abstand zum bisherigen Spannbaum gespeichert.
vorgänger[v]: Für jeden Knoten wird ein Elternelement gespeichert.
E und E': E ist die Menge aller Kanten des Eingabegraphen und E' ist die Menge der Kanten des sich entwickelnden minimalen Spannbaumes.
Ziel:
Nach der Ausführung des Prim-Algorithmus enthält E' alle Kanten eines minimalen Spannbaums von G. Da ein Spannbaum alle Knoten des Ausgangsgraphen enthält, muss für die Knoten keine zusätzliche Menge angelegt werden.
Initialisierung:
Der Startknoten bekommt als Abstandswert 0 zugewiesen, alle anderen Knoten ∞.
Allen Knoten wird als Vorgänger null zugewiesen.
Alle Knoten werden in Q eingefügt.
Schleife:
In jedem Schleifendurchlauf wird der Knoten u mit dem geringsten Abstand zum entstehenden Spannbaum aus Q extrahiert. Danach sieht man sich für jeden Nachbarn v∈Q von u an, ob der Abstand zwischen u und v kleiner ist als der Abstand zwischen v und dem bisherigen sich entwickelnden Graph. Wenn dem der Fall ist, werden abstand[v] und vorgänger[v] angepasst.
Beispiel
Als Beispiel soll wieder der Graph von weiter oben dienen mit A als Startknoten:
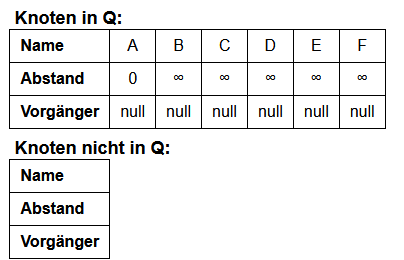
In der Initialisierungsphase vom Prim-Algorithmus werden alle Knoten in Q eingefügt und alle Knoten bekommen als Vorgänger null zugewiesen. Der Startknoten wird mit dem Abstandswert 0 initialisiert, alle anderen mit ∞.
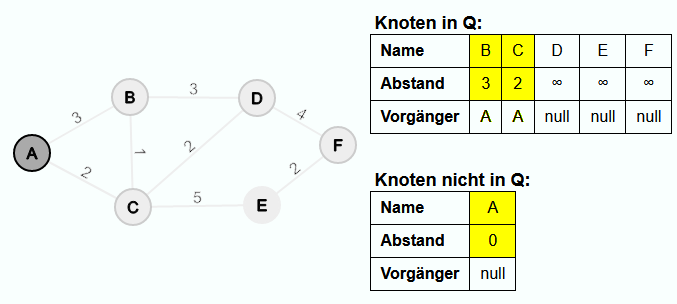
Der Startknoten A ist der Knoten in Q mit dem geringsten Abstandswert. Also wird A aus Q extrahiert.
A wird der Vorgänger von B und C und die Abstandswerte werden angepasst. Da A der Startknoten ist, wird keine Kante in E' eingefügt.
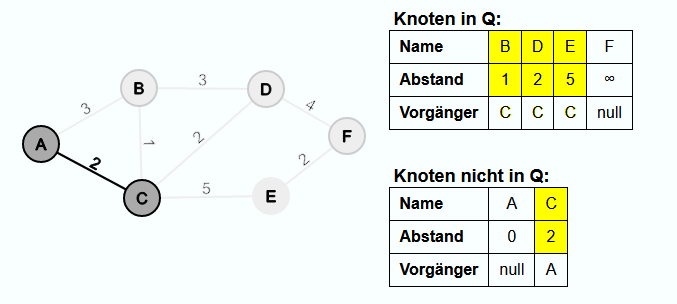
Als nächstes wird C aus Q extrahiert und die Kante {A, C} wird in E' eingefügt. Der Abstand von C zu B ist kleiner als der für B gespeicherte Abstandswert. Somit wird der Abstandswert auf das Gewicht der Kante {C, B} gesetzt und C wird der neue Vorgänger. Da für E und F noch keine Verbindung zum sich entwickelnden minimalen Spannbaum gefunden wurde, werden auch von diesen Knoten der Abstand und der Vorgänger angepasst.
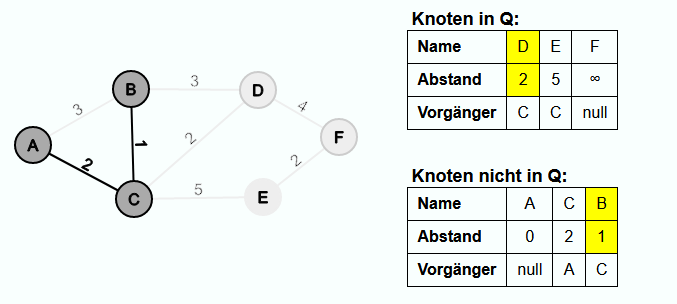
Danach wird B aus Q extrahiert und die Kante {C, B} wird in E' eingefügt. Der Abstand zu D ist nicht kleiner als der gespeicherte Wert, also wird in dieser Iteration nichts weiter gemacht.
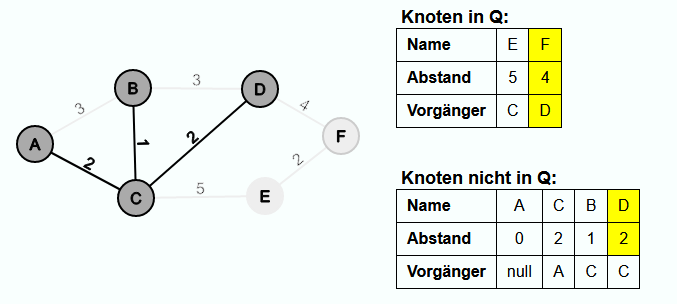
Nun wird D aus Q extrahiert und die Kante {C, D} wird in E' eingefügt. Es wurde die erste Verbindung zu F gefunden. Also wird D der neue Vorgängerknoten von F und der Abstand wird auf 4 gesetzt.
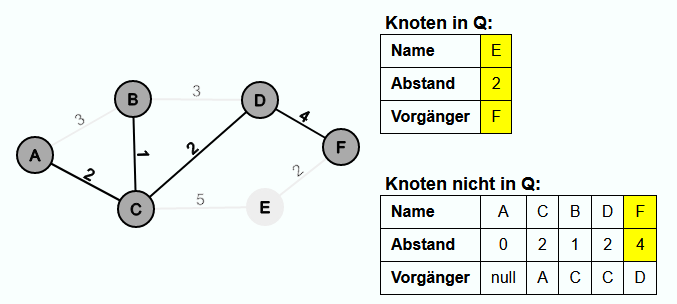
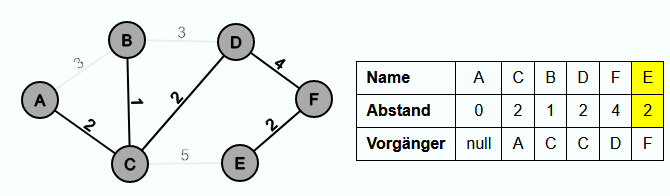
Dann wird F aus Q extrahiert und die Kante {D, F} wird in E' eingefügt. Da der Abstand zu E kleiner als 5 ist, wird F der neue Vorgänger von E und der Abstandswert von E wird auf 2 gesetzt.
In der letzten Iteration wird der Knoten E aus Q extrahiert und die Kante {F, E} wird in E' eingefügt.