Mit dem Sortieralgorithmus Quicksort lassen sich Listen und Arrays effizient sortieren. Der Algorithmus ist rekursiv und in jedem Rekursionsschritt werden die Elemente anhand von einem sogenannten Pivotelement umsortiert. Ein Pivotelement ist ein Element, welches zu Beginn vom Algorithmus ausgewählt wird und welches für den Algorithmus eine besondere Bedeutung bekommt.
Funktionsweise
Grundidee:
Bei einem Aufruf vom Quicksort-Algorithmus wird zuerst eines der Elemente im Array als Pivotelement festgelegt. Danach wird das Array so umsortiert, dass das Pivotelement an seiner finalen Position ist und alle Elemente, die kleiner als das Pivotelement sind, werden links vom Pivotelement eingefügt und alle Elemente, die größer sind, rechts. Ob Elemente, die gleich groß wie das Pivotelement sind links oder rechts vom Pivotelement eingefügt werden, ist egal. Danach wird Quicksort rekursiv sowohl auf das Teilarray links vom Pivotelement als auch auf das Teilarray rechts vom Pivotelement angewendet.
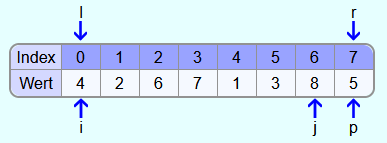
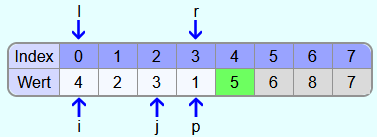
Angenommen das folgende Array soll mit Quicksort sortiert werden:
Wenn jetzt als Beispiel die 5 ganz rechts im Array als Pivotelement ausgewählt wird, wird das Array wie folgt umsortiert:
Die 5 steht nun an ihrer finalen Position. Danach wird Quicksort auf das Teilarray von Index 0 bis 3 und danach auf das Teilarray mit den Indizes 5 bis 7 aufgerufen.
Pseudocode:
Vorgehen:
Der Algorithmus erhält neben dem Array auch den Index von den Elementen ganz links und ganz rechts von dem Teilarray, welches mit Quicksort sortiert werden soll. Wenn das Teilarray nur ein Element oder kein Element enthält, kann der Algorithmus abgebrochen werden, weil Arrays mit weniger als 2 Elementen sind automatisch sortiert.
Zu Beginn wird ein Pivotelement gewählt. Im obigen Code wird immer das rechte Element als Pivotelement ausgewählt. Es könnte aber jedes beliebige Element im Teilarray als Pivotelement ausgewählt werden (Abschnitt: Wahl des Pivotelements). Außerdem werden 2 Variablen i und j definiert. i wird der Index vom Element ganz links im Array zugewiesen und j der Index vom Element links neben dem Pivotelement.
Nun wird der Index i so lange nach rechts versetzt, bis entweder ein Element gefunden wurde, welches größer als das Pivotelement ist oder bis j erreicht wurde. Danach wird j so lange nach links versetzt, bis ein Element gefunden wurde, welches kleiner als das Pivotelement ist oder bis i erreicht wurde. Wenn sowohl mit i ein Element gefunden wurde, welches größer als das Pivotelement ist, als auch mit j ein Element gefunden wurde, welches kleiner als das Pivotelement ist, werden diese vertauscht. Dies wird so lange gemacht, bis i und j auf das Gleiche Feld zeigen.
Abgesehen vom Pivotelement gibt es nun einen Bereich im Teilarray, in dem sich alle Elemente befinden, die kleiner als das Pivotelement sind, gefolgt von einem Teilbereich, in dem sich alle Elemente befinden, die größer als das Pivotelement sind. Elemente, die gleich dem Pivotelement sind, befinden sich entweder im einen oder im anderen Bereich.
Wenn es Elemente im Teilarray gibt, die größer als das Pivotelement sind, dann zeigt i nach der Schleife auf das am weitesten links liegende Feld in dem Bereich, in dem die Elemente größer als das Pivotelement sind. Dies liegt daran, dass mit i ein größeres Element gesucht wird, bevor mit j ein kleineres Element gesucht wird. In diesem Fall muss das Pivotelement mit dem Element mit dem Index i vertauscht werden.
Wenn es im Teilarray keine Elemente gibt, die größer als das Pivotelement sind, dann zeigt i nach der Schleife auf das Feld links vom Pivotelement und das Element in diesem Feld ist kleiner als das Pivotelement. In diesem Fall befindet sich das Pivotelement schon an der richtigen Stelle und muss nicht vertauscht werden.
Danach wird Quicksort mit dem Teilarray links vom Pivotelement aufgerufen und danach mit dem Teilarray rechts vom Pivotelement.
Beispiel:
Als Beispiel soll das Array von weiter oben sortiert werden. Als Pivotelement wird immer das rechte Element gewählt.
Aufruf Quicksort(A, 0, 7):
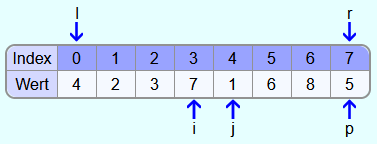
Es wird also der Quicksort-Algorithmus mit dem Index 0 als linke Schranke und dem Index 7 als rechte Schranke aufgerufen. Als Pivotelement wird die 5 gewählt. i zeigt auf das erste Element und j auf das Element links vom Pivotelement.
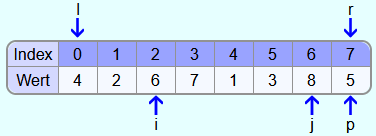
4 und 2 sind beide kleiner als das Pivotelement, also wird i 2 mal um 1 Feld weiter nach rechts versetzt. Die 6 ist größer als 5, also bleibt i bei der 6 stehen.
Jetzt wird sich die Zahl an der Stelle j angesehen. Die 8 ist größer als die 5 und somit wird j ein Feld weiter nach links gesetzt.
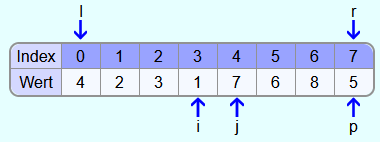
Da die 3 kleiner ist als die 5, bleibt j bei der 3 stehen. Nun werden die 6 und die 3 vertauscht.
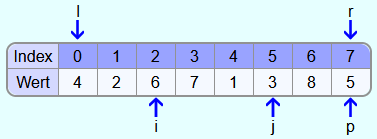
Jetzt wird wieder das Element an der Stelle i mit dem Pivotelement verglichen. 3 ist kleiner als 5. Also wird i um 1 weiter nach rechts gesetzt. 7 ist größer als 5 und somit bleibt i bei der 7 stehen.
Danach wird j mit dem Pivotelement verglichen. 6 ist größer als 5, also wird j 1 weiter nach links gesetzt. 1 ist kleiner als 5 und somit bleibt j bei der 1 stehen.
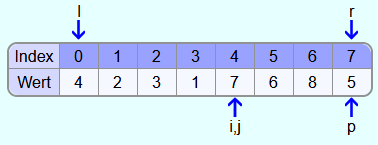
Die Zahlen in den Feldern i und j werden wieder vertauscht.
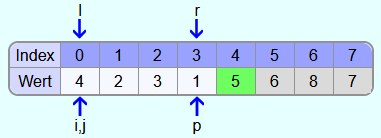
Es wird wieder die Zahl an der Stelle i mit dem Pivotelement verglichen. Da 1 kleiner ist, wird i ein Feld weiter nach rechts gesetzt.
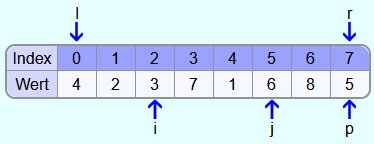
i und j zeigen jetzt auf das gleiche Feld. Also werden die Schleifen abgebrochen.
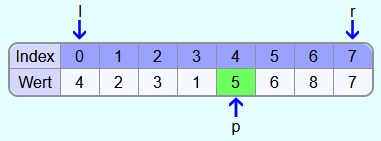
In den Feldern 0 bis 3 sind die Elemente nun kleiner als 5 und in den Feldern 4 bis 6 größer. Nun wird noch das Element an der Stelle i (also die 7) mit dem Pivotelement vertauscht.
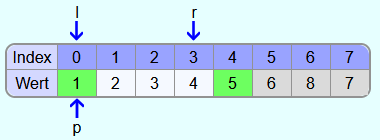
Die 5 befindet sich nun an der finalen Position und alle Elemente links davon sind kleiner und alle Elemente rechts davon sind größer.
Als nächstes wird Quicksort mit dem linken Teilarray aufgerufen und wenn dieser Aufruf abgearbeitet ist wird Quicksort mit dem rechten Teilarray aufgerufen.
Aufruf Quicksort(A, 0, 3):
Es wird wieder das rechte Element als Pivotelement ausgewählt. i wird auf das linke Element gesetzt und j auf das Elemente links vom Pivotelement.
Die 4 ist größer als das Pivotelement und deshalb bleibt i bei der 4 stehen. Da alle Elemente zwischen j und i größer sind als 1, wird j 3 mal um 1 Feld weiter nach links gesetzt, bis es sich auf dem selben Feld wie i befindet. Danach werden alle Schleifen abgebrochen.
Wieder wird das Pivotelement mit dem Element an der Stelle i vertauscht.
Auch die 1 befindet sich nun an der finalen Position. Als nächstes werden Quicksort(A, 0, -1) und danach Quicksort(A, 1, 3) aufgerufen.
Aufruf Quicksort(A, 0, -1):
Dieser Aufruf wird abgebrochen, weil der linke Index nicht kleiner als der rechte Index ist.
Ergebnis:
Nach dem Aufruf von Quicksort(A, 0, -1) wird Quicksort(A, 1, 3) aufgerufen. Wenn dieser Aufruf abgearbeitet ist, wird noch der Aufruf Quicksort(A, 5, 7) aus dem ersten Aufruf abgearbeitet. Da das sehr redundant ist und den Rahmen komplett sprengen würde, kürze ich das ab und zeige direkt das Ergebnis:
Wahl des Pivotelements:
Bisher wurde immer nur das rechte Element aus dem Teilarray als Pivotelement ausgewählt. Im Prinzip könnte sich aber auch für ein beliebiges anderes Element aus dem Teilarray entschieden werden. Gerne genommen wird zum Beispiel auch das Element in der Mitte. Dann sollte aber vor der Initialisierung von i und j das Pivotelement mit dem rechten Element vertauscht werden.
Aber warum sollte man sich diesen zusätzlichen Aufwand machen? Der Quicksort-Algorithmus wird besonders effizient, wenn sich nach dem Umsortieren auf beiden Seiten vom Pivotelement ähnlich viele Elemente befinden. Wenn immer das rechte Element als Pivotelement gewählt wird und wenn das Array, welches sortiert werden soll, schon sortiert ist, dann bleiben nach dem Umsortieren alle Elemente links vom Pivotelement stehen. In diesem Fall ist die Laufzeitkomplexität quadratisch.
Um dies zu verhindern sollte man, wenn das Array teilweise vorsortiert ist, das mittlere Element oder ein zufälliges Element als Pivotelement wählen.