Selectionsort ist ein einfacher Sortieralgorithmus mit einer quadratischen Laufzeit (O(n2)).
Funktionsweise
Grundidee:
Das Array besteht aus einem sortierten Teil gefolgt von einem noch nicht sortierten Teil. Die Felder im sortierten Teil enthalten die Elemente, die auch das sortierte Array nach der Ausführung vom Algorithmus enthalten wird. Vor der i-ten Iteration besteht der sortierte Bereich aus den ersten i-1 Elementen des Arrays. Nach der i-ten Iteration soll das i-te Feld vom Array das kleinste Element aus dem unsortierten Teil enthalten. Somit enthalten nach der i-ten Iteration die ersten i Felder das richtige Element.
Dies wird erreicht, indem in jeder Iteration alle Elemente vom unsortierten Teil nach dem kleinsten Element durchsucht werden und wenn nicht das i-te Element das kleinste Element ist, werden das kleinste und das i-te Element vertauscht.
Angenommen das Array sieht nach der zweiten Iteration wie folgt aus:
Die beiden ersten beiden Elemente befinden sich schon im richtigen Feld. In der 3ten Iteration wird der unsortierte Teil vom Array (also die weißen Felder) nach dem kleinsten Element durchsucht. Das ist die 3. Also werden die 3 und die 8 vertauscht. Danach sind die ersten 3 Elemente an der richtigen Position.
Pseudocode:
Vorgehen:
Es wird mit einem Index i von 0 beginnend über alle Felder des Arrays iteriert (mit Ausnahme vom letzten Feld). In jeder Iteration ist zuerst das Element mit dem Index i das kleinste im unsortierten Bereich gefundene Element. Dann wird mit der Hilfe von einem Index j über alle Felder hinter dem i-ten Feld iteriert und jedesmal, wenn das Element mit dem Index j kleiner ist, als das bisher kleinste gefundene Element, wird das Element mit dem Index j das neue kleinste gefundene Element.
Wenn nach der Iteration über alle Elemente aus dem unsortierten Teil das kleinste Element sich noch nicht an der Stelle i befindet, werden das kleinste Element und das Element an der Stelle i vertauscht.
Wenn sich nur noch ein Element im unsortierten Bereich befindet, befindet sich auch dieses automatisch an der richtigen Stelle und der Algorithmus kann beendet werden.
kleines Beispiel:
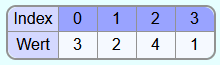
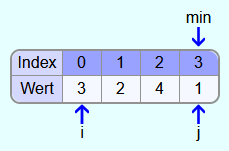
Als Beispiel soll das folgende Array mit Selectionsort sortiert werden:
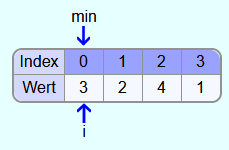
Iteration 1:
In der ersten Iteration ist i=0 (Wert 3). Das erste Element wird am Anfang dieser Iteration auch zum kleinsten bisher gefundenen Element min.
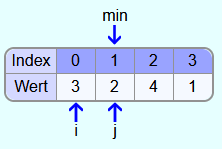
Danach wird mit dem Index j über alle Felder hinter dem Feld mit dem Index i iteriert. Zuerst wird überprüft, ob das Element mit dem Index 1 kleiner ist, als das Element an der Stelle min. Das ist der Fall (2<3) und somit ist das Element mit dem Index 1 das neue kleinste Element.
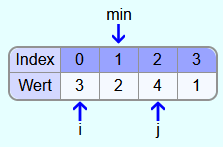
Danach werden die Elemente mit den Indizes 1 und 2 verglichen. Da 4 nicht kleiner als 2 ist, wurde kein neues kleinstes Element gefunden.
Da 1 kleiner als 2 ist, bekommt min im nächsten Schritt den Index 3.
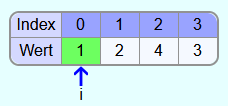
Das kleinste gefundene Element befindet sich noch nicht an der Stelle i. Also werden das Element an der Stelle i und das Element an der Stelle min vertauscht.
Der sortierte Teil vom Array besteht nun aus dem Feld mit dem Index 0 und der unsortierte Teil aus den Feldern mit den Indizes 1-3.
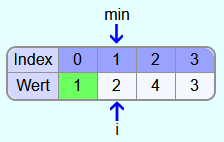
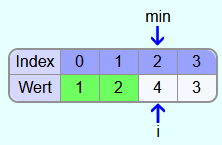
Iteration 2:
Als nächstes wird das Element im Feld mit dem Index 1 das das neue kleinste Element.
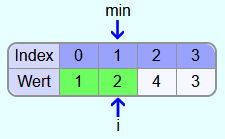
Da 2 kleiner ist als 4 und 3, wird min nach dem Vergleich mit den Elementen mit den Indizes 2 und 3 nicht verändert. Somit befindet sich im Feld mit dem Index i schon das richtige Element und es müssen in der Iteration keine Elemente vertauscht werden.
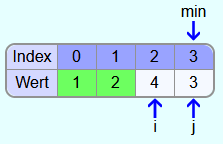
Iteration 3:
In Iteration 3 wird das werden die Indizes i und min auf 2 gesetzt.
Da 3 kleiner als 4 ist, wird das Element mit dem Index 3 das neue kleinste Element mit dem Index min.
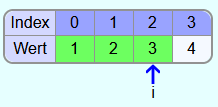
Das Feld mit dem Index i enthält noch nicht das kleinste Element. Also werden die 3 und die 4 vertauscht.
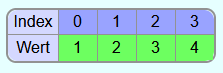
Ergebnis:
Der unsortierte Bereich enthält nur noch 1 Element und ein einelementiger Teilbereich ist immer automatisch sortiert. Somit ist das gesamte Array nun sortiert.
umgekehrte Sortierreihenfolge
Der Selectionsort-Algorithmus lässt sich sehr einfach so anpassen, dass die Elemente nicht in aufsteigender Reihenfolge, sondern beginnend mit dem größten Element in absteigender Reihenfolge sortiert werden. Dazu muss im unsortierten Bereich nicht nach dem kleinsten Element sondern nach dem größten gesucht werden.